Parmi la variété de formes géométriques, un quadrilatère tel qu'un losange se distingue. Même son nom lui-même n'est pas typique pour la désignation de quadrangles. Et bien qu'en géométrie il soit beaucoup moins courant que de tels formes simples comme un cercle, un triangle, un carré ou un rectangle, il ne peut pas non plus être ignoré.
Vous trouverez ci-dessous la définition, les propriétés et les caractéristiques des losanges.
Définition
Un losange est un parallélogramme avec côtés égaux... Un losange est appelé carré si tous ses coins sont droits. L'exemple le plus frappant d'un losange est l'image d'un costume de diamant sur une carte à jouer. De plus, le losange était souvent représenté sur divers blasons. Un exemple de losange dans Vie courante peut servir de terrain de basket.
Propriétés
- Les côtés opposés du losange se trouvent sur des lignes parallèles et ont la même longueur.
- L'intersection des diagonales du losange se produit à un angle de 90 ° en un point, qui est leur milieu.
- Les diagonales du losange coupent en leur milieu le coin du haut duquel elles sont sorties.
- Sur la base des propriétés du parallélogramme, vous pouvez déduire la somme des carrés des diagonales. D'après la formule, il est égal au côté élevé à la puissance quadratique et multiplié par quatre.
Panneaux
Nous devons clairement comprendre que tout losange est un parallélogramme, mais en même temps, tous les parallélogrammes n'ont pas tous les indicateurs d'un losange. Pour distinguer ces deux formes géométriques, vous devez connaître les signes d'un losange. Énumérés ci-dessous signes caractéristiques une forme géométrique donnée :
- Deux côtés ayant un sommet commun sont égaux.
- Les diagonales se coupent à un angle de 90 ° C.
- Au moins une diagonale divise les angles des sommets desquels elle émerge en deux.
Formules de zone
Formule de base :
- S = (CA * BD) / 2
D'après les propriétés du parallélogramme :
- S = (AB * H AB)
Basé sur la valeur de l'angle entre deux côtés adjacents du losange :
- S = AB2 * sinα
Si l'on connaît la longueur du rayon d'un cercle inscrit dans un losange :
- S = 4r 2 / (sinα), où :
- S - zone;
- AB, AC, BD - désignation des parties ;
- H - hauteur;
- r est le rayon du cercle ;
- sinα - sinus alpha.
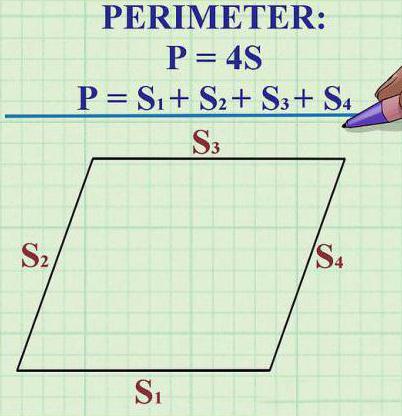
Périmètre
Pour calculer le périmètre d'un losange, il suffit de multiplier la longueur de l'un de ses côtés par quatre.
Construction de dessin
Certains ont du mal à construire un motif en losange. Même si vous avez déjà compris ce qu'est un losange, on ne sait pas toujours comment construire son dessin avec précision et dans le respect des proportions nécessaires.
Il existe deux façons de créer un motif en losange :
- Tout d'abord, construisez une diagonale, puis la deuxième diagonale perpendiculaire à celle-ci, puis connectez les extrémités des segments des côtés parallèles par paires adjacents du losange.
- Tout d'abord, placez un côté du losange, puis, parallèlement à celui-ci, construisez un segment de longueur égale et connectez les extrémités de ces segments également en parallèle par paires.
Soyez prudent lors de la construction - si dans l'image vous faites la même longueur de tous les côtés du losange, vous n'obtiendrez pas un losange, mais un carré.
Définition
Un losange est un quadrilatère dont tous les côtés sont égaux.
Commenter
Un losange est un cas particulier de parallélogramme, car ses côtés opposés sont égaux deux à deux (troisième caractéristique).
Commenter
Le diamant hérite de toutes les propriétés du parallélogramme.
Propriétés du diamant
Les diagonales du losange sont perpendiculaires entre elles.
Les diagonales d'un losange sont les bissectrices de ses angles.
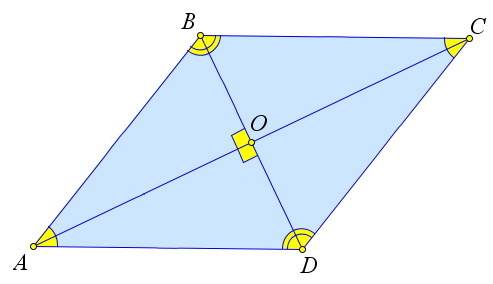
Preuve
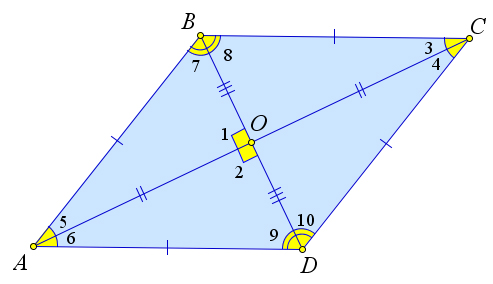
Considérons un losange $ ABCD $ dans lequel les diagonales $ AC $ et $ BD $ se rencontrent au point $ O $.
Montrons qu'elles sont perpendiculaires et bissectrices des angles du losange.
En effet, puisque $ ABCD $ est un cas particulier de parallélogramme, les diagonales sont divisées par le point d'intersection en deux, c'est-à-dire $ AO = OC, BO = OD $.
Alors, puisque $ AB = BC = CD = DA $, alors $ \ triangle AOB = \ triangle BOC = \ triangle COD = \ triangle AOD $ par le troisième signe d'égalité.
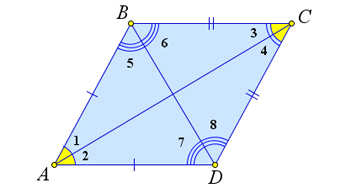
Alors $ \ angle 1 = \ angle 2 = 90 ^ \ circ $ puisque ce sont des angles adjacents.
Aussi, $\angle 3 = \angle 4 = \angle 5 = \angle 6$, $\angle 7 = \angle 8 = \angle 9 = \angle 10$.
Ainsi, les diagonales sont perpendiculaires et sont les bissectrices des angles du losange.
Conséquence
Les diagonales du losange le divisent en quatre triangles rectangles égaux.
Signes d'un losange
Si les diagonales d'un parallélogramme sont perpendiculaires entre elles, alors ce parallélogramme est un losange.
Si l'une des diagonales d'un parallélogramme est la bissectrice de son angle, alors ce parallélogramme est un losange.
Si dans le quadrilatère $ ABCD $ la diagonale $ AC $ est la bissectrice des angles $ \ angle A $ et $ \ angle C $, et la diagonale $ BD $ est la bissectrice des angles $ B $ et $ D $, alors $ ABCD $ est un losange.
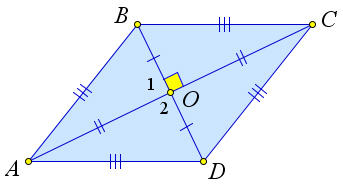
Preuve
Démontrons le premier élément du théorème.
Considérons un parallélogramme $ ABCD $ avec $ AC \ perp BD $.
Montrons que $ ABCD $ est un losange.
Dans un parallélogramme, le point d'intersection est divisé en deux, donc $ AO = OC, BO = OD $.
Aussi, $ \ angle 1 = \ angle 2 = 90 ^ \ circ $.
Alors $ \ triangle AOB = \ triangle AOD $ par le premier signe d'égalité.
D'où $AB = AD$.
Et puisque $ ABCD $ est un parallélogramme, alors $ BC = AD = AB = CD $, c'est-à-dire que $ ABCD $ est un losange.
Démontrons la deuxième partie du théorème.
Considérons un parallélogramme $ ABCD $ dans lequel la diagonale $ AC $ est la bissectrice de l'angle $ \ angle A $, c'est-à-dire $ \ angle 1 = \ angle 2 $.
Montrons que $ ABCD $ est un losange.
$ \ angle 2 = \ angle 3 $, comme entrecroisé, donc, $ \ angle 1 = \ angle 3 $.
C'est-à-dire que $ \ triangle ABC $ est isocèle et $ AB = BC $.
Et puisque $ ABCD $ est un parallélogramme, alors $ AB = CD, BC = AD $, c'est-à-dire $ AB = BC = CD = AD $, et $ ABCD $ est un losange.
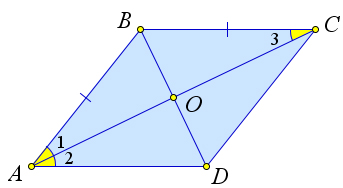
Démontrons la troisième partie du théorème
Notez que $ \ triangle ABC = \ triangle ADC $ par le deuxième attribut ($ \ angle 1 = \ angle 2, \ angle 3 = \ angle 4 $, $ AC $ est total).
Alors $ \ angle B = \ angle D $, et par conséquent, leurs moitiés sont également égales : $ \ angle 5 = \ angle 6 = \ angle7 = \ angle 8 $.
Mais alors les triangles $\triangle ABD$ et $\triangle BCD$ sont isocèles : $AB = AD, BC = CD$.
De plus, $\triangle ABD = \triangle BCD$ sur la seconde base ($ BD$ - total, $\angle 5 = \angle6, \angle 7 = \angle 8$).
Donc $ AB = BC $ et $ AD = CD $.
Ainsi, tous les côtés du quadrilatère sont égaux entre eux : $ AB = BC = CD = DA $.
Un losange est un quadrilatère dont les côtés sont égaux et parallèles deux à deux. Contrairement à un carré dont les coins sont droits, un losange a deux coins aigus et deux coins obtus, situés sur des côtés opposés. Mais les diagonales se coupent à angle droit et sont en même temps bissectrices. Le point d'intersection des diagonales les divise en parties égales.
Il existe de nombreuses formules pour trouver les diagonales d'un losange, il suffit de connaître les données initiales et de choisir la bonne.
Comment trouver la diagonale d'un losange par le côté et l'angle : lorsque les côtés et l'un des coins du losange sont connus, les formules suivantes sont appliquées : Par le côté et le demi-angle :
La somme des carrés des diagonales est égale au carré du côté multiplié par quatre D ^ 2 + d ^ 2 = 4a ^ 2. De là on peut déduire que :
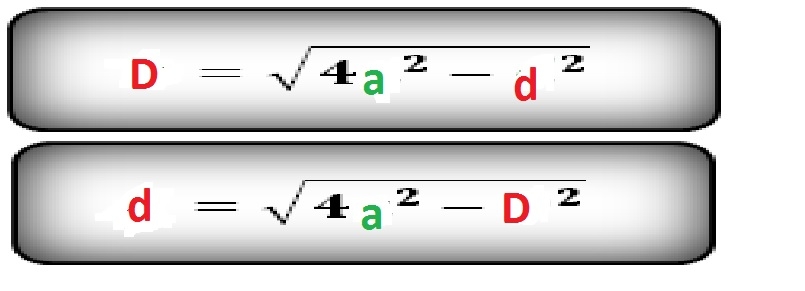

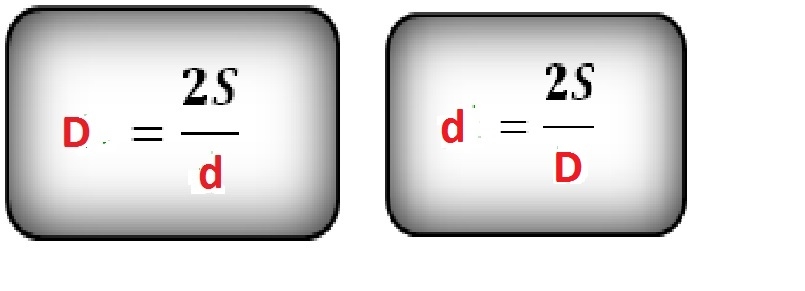
Trouvez la plus petite diagonale du losange, si le périmètre est de 20 cm, la plus grande diagonale est de 8 cm.
Soit : P = 20 cm, D = 8 cm. Trouvez la longueur d'un côté du losange en divisant le périmètre par quatre a = 20/4 = 5 cm. Utilisons la formule du point 3 et obtenons d = (4 * 5 ^ 2-8 ^ 2) ^ 1/2 = 6 cm.
Malgré l'apparente simplicité d'une figure géométrique telle qu'un losange, elle regorge de nombreux moments intéressants. Les propriétés d'un parallélogramme, d'une bissectrice, d'un triangle rectangle et parfois d'un triangle isocèle lui sont applicables. Connaissant les formules, vous pouvez facilement résoudre le problème de trouver les diagonales d'un losange.
Un losange est une forme particulière en géométrie. En raison de ses propriétés particulières, il n'y a pas une, mais plusieurs formules qui peuvent être utilisées pour calculer l'aire d'un losange. Quelles sont ces propriétés et quelles sont les formules les plus courantes pour trouver l'aire de cette forme ? Trouvons-le.
Quelle forme géométrique s'appelle un losange
Avant de savoir quelle est l'aire du losange, il vaut la peine de savoir de quel type de figure il s'agit.
Depuis l'époque de la géométrie euclidienne, un losange est appelé un quadrilatère symétrique, dont les quatre côtés sont de longueur égale et parallèles deux à deux.
Origine du terme
Le nom de cette figure est venu dans la plupart des langues modernes du grec, par la médiation du latin. L'« ancêtre » du mot « losange » était le nom grec ῥόμβος (tambourin). Bien que les habitants du XXe siècle, habitués aux tambourins ronds, aient du mal à imaginer leur autre forme, mais chez les Grecs, ces instruments de musique n'étaient traditionnellement pas ronds, mais en forme de losange.
Dans la plupart des langues modernes, ce terme mathématique est utilisé, comme en latin : rombus. Cependant, dans langue Anglaise parfois les losanges sont appelés diamant (diamant ou diamant). Ce chiffre a reçu un tel surnom en raison de sa forme particulière, qui rappelle Pierre précieuse... En règle générale, un terme similaire n'est pas utilisé pour tous les losanges, mais uniquement pour ceux dans lesquels l'angle d'intersection de ses deux côtés est égal à soixante ou quarante-cinq degrés.
Ce chiffre a été mentionné pour la première fois dans les écrits d'un mathématicien grec qui a vécu au premier siècle nouvelle ère- Héros d'Alexandrie.
Quelles propriétés possède cette figure géométrique ?
Pour trouver l'aire d'un losange, il faut d'abord savoir quelles sont les caractéristiques d'un figure géométrique. 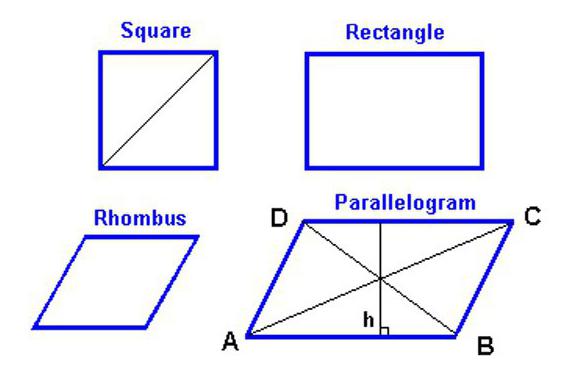
Dans quelles conditions un parallélogramme est-il un losange
Comme vous le savez, chaque losange est un parallélogramme, mais tous les parallélogrammes ne sont pas un losange. Pour affirmer avec précision que la figure présentée est bien un losange, et non un simple parallélogramme, elle doit correspondre à l'une des trois caractéristiques principales qui distinguent un losange. Ou les trois à la fois.
- Les diagonales du parallélogramme se coupent à un angle de quatre-vingt-dix degrés.
- Les diagonales divisent les coins en deux, agissant comme leurs bissectrices.
- Non seulement les côtés parallèles mais aussi adjacents sont de la même longueur. C'est d'ailleurs l'une des principales différences entre un losange et un parallélogramme, car la deuxième figure n'a que des côtés parallèles de même longueur, mais pas adjacents.
Dans quelles conditions un losange est-il un carré
Selon ses propriétés, dans certains cas, un losange peut devenir simultanément un carré. Pour confirmer visuellement cette affirmation, il suffit de faire pivoter le carré dans n'importe quelle direction de quarante-cinq degrés. La figure résultante se révélera être un losange, dont chacun des coins est égal à quatre-vingt-dix degrés.
Aussi, pour confirmer que le carré est un losange, vous pouvez comparer les caractéristiques de ces figures : dans les deux cas, tous les côtés sont égaux et les diagonales sont des bissectrices et se coupent à un angle de quatre-vingt-dix degrés.
Comment connaître l'aire d'un losange à l'aide de ses diagonales
V monde moderne sur Internet, vous pouvez trouver presque tous les matériaux pour effectuer les calculs nécessaires. Ainsi, il existe de nombreuses ressources équipées de programmes permettant de calculer automatiquement l'aire d'une figure particulière. De plus, s'il existe (comme dans le cas d'un losange) plusieurs formules pour cela, il est alors possible de choisir celle qui sera la plus pratique à utiliser. Cependant, tout d'abord, vous devez être capable de calculer vous-même l'aire d'un losange sans l'aide d'un ordinateur et de naviguer dans les formules. Il y en a beaucoup pour un losange, mais les plus célèbres d'entre eux sont au nombre de quatre. 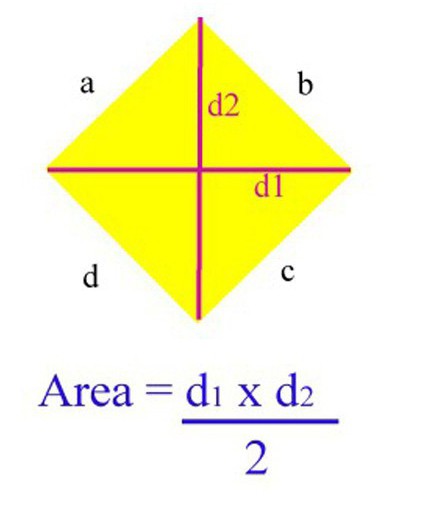
L'un des moyens les plus simples et les plus courants de connaître l'aire de cette figure, s'il existe des informations sur la longueur de ses diagonales. Si le problème contient ces données, dans ce cas, vous pouvez appliquer la formule suivante pour trouver l'aire : S = KM x LN / 2 (KM et LN sont les diagonales du losange KLMN).
Vous pouvez tester la validité de cette formule dans la pratique. Supposons que le losange KLMN a la longueur de l'une de ses diagonales KM - 10 cm et le second LN - 8 cm. Ensuite, nous substituons ces données dans la formule ci-dessus et nous obtenons le résultat suivant : S = 10 x 8/2 = 40cm2.
Formule pour calculer l'aire d'un parallélogramme
Il existe également une autre formule. Comme mentionné ci-dessus dans la définition d'un losange, ce n'est pas seulement un quadrilatère, mais aussi un parallélogramme, et a toutes les caractéristiques de cette figure. Dans ce cas, pour trouver son aire, il convient tout à fait d'utiliser la formule utilisée pour le parallélogramme : S = KL x Z. Dans ce cas, KL est la longueur du côté du parallélogramme (losange), et Z est le longueur de la hauteur tirée de ce côté. 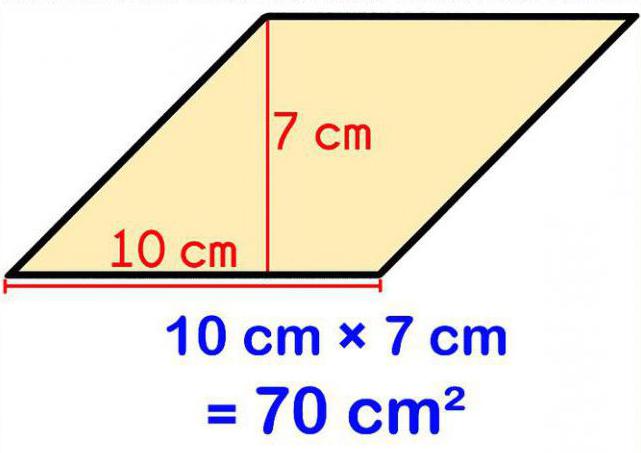
Dans certains problèmes, la longueur du côté n'est pas fournie, mais le périmètre du losange est connu. Puisque la formule pour le trouver a été indiquée ci-dessus, vous pouvez l'utiliser pour connaître la longueur du côté. Ainsi, le périmètre de la figure est de 10 cm.La longueur du côté peut être trouvée en inversant la formule du périmètre et en divisant 10 par 4. Le résultat est de 2,5 cm - c'est la longueur souhaitée du côté du losange.
Maintenant, cela vaut la peine d'essayer de substituer ce nombre dans la formule, sachant que la longueur de la hauteur dessinée sur le côté est également de 2,5 cm.Essayons maintenant de mettre ces valeurs dans la formule ci-dessus pour l'aire d'un parallélogramme. Il s'avère que l'aire du losange est S = 2,5 x 2,5 = 6,25 cm 2.
Autres façons de calculer l'aire d'un losange
Ceux qui maîtrisent déjà les sinus et les cosinus peuvent utiliser des formules les contenant pour trouver l'aire d'un losange. Un exemple classique est la formule suivante : S = KM 2 x Sin KLM. Dans ce cas, l'aire de la figure est égale au produit des deux côtés du losange multiplié par le sinus de l'angle qui les sépare. Et comme dans un losange tous les côtés sont les mêmes, il est plus facile de produire immédiatement un côté en carré, comme le montre la formule.
Nous vérifions ce schéma dans la pratique, et pas seulement à un losange, mais à un carré, dans lequel, comme vous le savez, tous les angles sont droits, ce qui signifie qu'ils sont égaux à quatre-vingt-dix degrés. Disons que l'un des côtés mesure 15 cm.On sait aussi que le sinus d'un angle de 90 ° est égal à un. Ensuite, selon la formule, S = 15 x 15 x Sin 90° = 255x1 = 255 cm 2.
En plus de ce qui précède, dans certains cas, une autre formule est utilisée, utilisant un sinus pour déterminer l'aire d'un losange : S = 4 x R 2 / Sin KLM. Dans cette version, le rayon du cercle inscrit dans le losange est utilisé. Il s'élève à la puissance du carré et se multiplie par quatre. Et l'ensemble du résultat est divisé par le sinus de l'angle le plus proche de la figure inscrite.
A titre d'exemple, pour simplifier les calculs, nous reprenons un carré (le sinus de son angle sera toujours égal à un). Le rayon du cercle qui y est inscrit est de 4,4 cm, alors l'aire du losange sera calculée comme suit : S = 4 x 4,4 2 / Sin 90° = 77,44 cm 2
Les formules ci-dessus pour trouver le rayon d'un losange sont loin d'être uniques, mais elles sont les plus faciles à comprendre et à effectuer des calculs.
B. A. S. D. Une propriété spéciale d'un losange. Les diagonales d'un losange sont perpendiculaires entre elles et divisent par deux ses coins. Donné : losange ABCD. Puisque le losange est un parallélogramme, alors BO = DO. Ensuite, AO est la médiane. AO - hauteur. AO est une bissectrice.
Diapositive 11 de la présentation "Types de rectangles"... La taille de l'archive avec la présentation est de 275 Ko.Géométrie grade 8
résumé autres présentations"" Triangles similaires "grade 8" - Moyenne proportionnelle. Signes de similitude des triangles. Triangles similaires. Deuxième signe. Cosinus. О - l'intersection des médianes. Dans la vie de tous les jours, il existe des objets de la même forme. Tâche. Jambe d'un triangle rectangle. Segments. Ligne médiane. ASN et VSN sont rectangulaires. Médianes dans un triangle. Hauteur dans un triangle. Sinus d'un angle aigu d'un triangle rectangle. Définition de triangles semblables.
"Les théorèmes de Cheva et Ménélas" - Points. Le théorème de Cheva. Biographie du scientifique. Théorème de Ménélas. Point K. Les théorèmes de Cheva et Ménélas. Dessinons des lignes droites. Droite parallèle à la bissectrice. Solution. Ménélas d'Alexandrie. Point. Segments. Égalité. VM-médiane. Côté milieu. Le contraire du théorème.
"Trouver l'aire d'un parallélogramme" - Trouver l'aire d'un parallélogramme. Signes d'égalité triangles rectangles... Aire d'un triangle. Hauteur. Détermination de la hauteur du parallélogramme. Trouvez l'aire du rectangle. Propriétés des zones. Trouvez l'aire du triangle. Zone carrée. Trouvez l'aire du carré. Zone de parallélogramme. Hauteurs de parallélogramme. Exercices oraux. Trouvez le périmètre du carré. Base.
"Construction d'une tangente à un cercle" - Le théorème sur les segments de tangentes. Un cercle et une droite ont un point commun. Répétition. Cercle. Des points communs. Solution. La position relative de la droite et du cercle. Diamètre. Circonférence et ligne droite. Accord. La tangente au cercle.
"" Cercle "géométrie" - Théorème sur un cercle inscrit dans un triangle. Bissectrices d'un triangle. La tangente au cercle. Propriétés des côtés d'un quadrilatère circonscrit à un cercle. Théorème perpendiculaire au centre. Un angle dont le sommet se trouve sur un cercle. Théorème de la bissectrice. Coin central. Une droite qui n'a qu'un point commun avec un cercle. Propriétés des coins d'un quadrilatère inscrit dans un cercle.
"Solution du théorème de Pythagore" - Hammurabi. Carré. Diamètre. Zone carrée. Hexagones. Géométrie. Applications du théorème de Pythagore. Hauteur. La preuve d'Epstein. Triangles. Biographie de Pythagore. Preuve de soustraction. Preuve complète. Preuve par la méthode d'expansion. Preuve du 9ème siècle après JC Motif. Théorème de Pythagore. Chantre. La preuve de Gutheil. La preuve de Nielsen. Énoncé du théorème. Pythagoriciens.
