Iš geometrinių formų įvairovės išsiskiria toks keturkampis kaip rombas. Net pats jo pavadinimas nėra būdingas keturkampiams žymėti. Ir nors geometrijoje tai daug rečiau nei tokia paprastos formos kaip apskritimas, trikampis, kvadratas ar stačiakampis, jo taip pat negalima ignoruoti.
Žemiau pateikiamas rombų apibrėžimas, savybės ir savybės.
Apibrėžimas
Rombas yra lygiagretainis su lygios pusės... Rombas vadinamas kvadratu, jei visi jo kampai yra tiesūs. Ryškiausias rombo pavyzdys yra deimantinio kostiumo vaizdas žaidimo kortoje. Be to, rombas dažnai buvo vaizduojamas įvairiuose herbuose. Rombo pavyzdys Kasdienybė gali tarnauti kaip krepšinio aikštelė.
Savybės
- Priešingos rombo pusės yra lygiagrečiose linijose ir yra vienodo ilgio.
- Rombo įstrižainės susikerta 90 ° kampu viename taške, o tai yra jų vidurio taškas.
- Rombo įstrižainės dalija kampą, iš kurio viršaus jos išėjo.
- Remdamiesi lygiagretainio savybėmis, galite nustatyti įstrižainių kvadratų sumą. Pagal formulę ji lygi kraštinei, pakeltai iki kvadratinės galios ir padauginta iš keturių.
Ženklai
Turime aiškiai suprasti, kad bet kuris rombas yra lygiagretainis, tačiau tuo pat metu ne kiekvienas lygiagretainis turi visus rombo rodiklius. Norėdami atskirti šias dvi geometrines figūras, turite žinoti rombo ženklus. Išvardinta žemiau būdingi ženklai nurodyta geometrinė forma:
- Bet kurios dvi kraštinės, turinčios bendrą viršūnę, yra lygios.
- Įstrižainės susikerta 90 ° C kampu.
- Bent viena įstrižainė dalija kampus iš viršūnių taškų, iš kurių ji išeina.
Ploto formulės
Pagrindinė formulė:
- S = (AC * BD) / 2
Remiantis lygiagretainio savybėmis:
- S = (AB * H AB)
Remiantis kampo tarp dviejų gretimų rombo kraštinių verte:
- S = AB2 * sinα
Jei žinome į rombą įbrėžto apskritimo spindulio ilgį:
- S = 4r 2 / (sinα), kur:
- S - plotas;
- AB, AC, BD - šalių nurodymas;
- H - aukštis;
- r yra apskritimo spindulys;
- sinα – sinuso alfa.
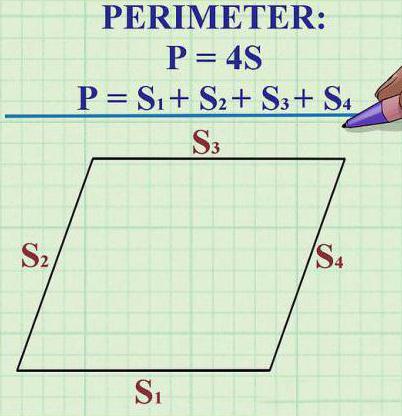
Perimetras
Norėdami apskaičiuoti rombo perimetrą, tereikia bet kurios jo kraštinės ilgį padauginti iš keturių.
Brėžinio konstrukcija
Kai kuriems sunku sukurti deimantinį raštą. Net jei jau supratote, kas yra rombas, ne visada aišku, kaip tiksliai ir laikantis reikiamų proporcijų sukonstruoti jo brėžinį.
Yra du būdai sukurti deimantinį raštą:
- Pirmiausia sukonstruokite vieną įstrižainę, po to antrą jai statmeną įstrižainę, o tada sujunkite gretimų porų lygiagrečių rombo kraštinių segmentų galus.
- Pirmiausia uždėkite vieną rombo kraštą, tada lygiagrečiai jai sukonstruokite vienodo ilgio atkarpą, o šių atkarpų galus taip pat lygiagrečiai sujunkite poromis.
Būkite atsargūs statydami – jei paveikslėlyje padarysite vienodą visų rombo kraštinių ilgį, gausite ne rombą, o kvadratą.
Apibrėžimas
Rombas yra keturkampis, kurio visos kraštinės yra lygios.
komentuoti
Rombas yra ypatingas lygiagretainio atvejis, nes jo priešingos kraštinės yra poromis lygios (trečias požymis).
komentuoti
Deimantas paveldi visas lygiagretainio savybes.
Deimantų savybės
Rombo įstrižainės yra viena kitai statmenos.
Rombo įstrižainės yra jo kampų pusiausvyros.
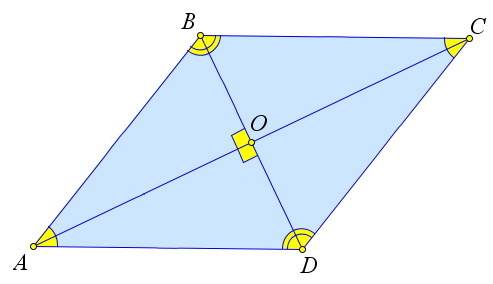
Įrodymas
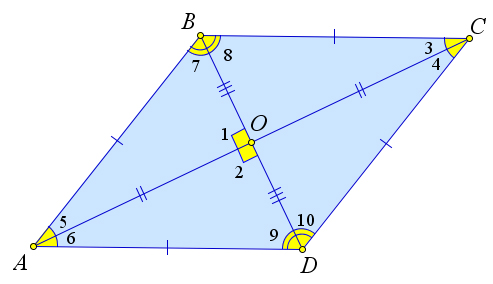
Apsvarstykite rombą $ ABCD $, kuriame įstrižainės $ AC $ ir $ BD $ susikerta taške $ O $.
Įrodykime, kad jie yra statmeni ir yra rombo kampų pusiausvyros.
Iš tiesų, kadangi $ ABCD $ yra ypatingas lygiagretainio atvejis, įstrižainės dalijamos iš susikirtimo taško per pusę, tai yra $ AO = OC, BO = OD $.
Tada, kadangi $ AB = BC = CD = DA $, tada $ \ trikampis AOB = \ trikampis BOC = \ trikampis COD = \ trikampis AOD $ trečiuoju lygybės ženklu.
Tada $ \ kampas 1 = \ kampas 2 = 90 ^ \ circ $, nes tai yra gretimi kampai.
Taip pat $ \ kampas 3 = \ kampas 4 = \ kampas 5 = \ kampas 6 $, $ \ kampas 7 = \ kampas 8 = \ kampas 9 = \ kampas 10 $.
Taigi, įstrižainės yra statmenos ir yra rombo kampų pusiausvyros.
Pasekmė
Rombo įstrižainės padalija jį į keturis vienodus stačiakampius trikampius.
Rombo ženklai
Jei lygiagretainio įstrižainės yra viena kitai statmenos, tai šis lygiagretainis yra rombas.
Jei viena iš lygiagretainio įstrižainių yra jo kampo pusiausvyra, tai šis lygiagretainis yra rombas.
Jei keturkampyje $ ABCD $ įstrižainė $ AC $ yra kampų $ \ kampas A $ ir $ \ kampas C $, o įstrižainė $ BD $ yra kampų $ B $ ir $ D $ pusiausvyra, tada $ ABCD $ yra rombas.
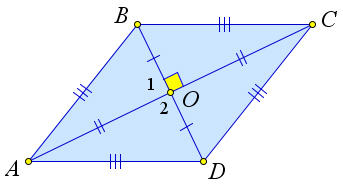
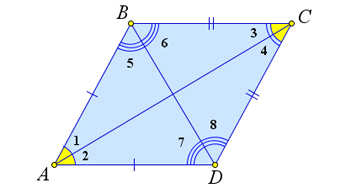
Įrodymas
Įrodykime pirmąjį teoremos punktą.
Apsvarstykite lygiagretainį $ ABCD $ su $ AC \ perp BD $.
Įrodykime, kad $ ABCD $ yra rombas.
Lygiagretainyje susikirtimo taškas padalintas per pusę, todėl $ AO = OC, BO = OD $.
Taip pat $ \ kampas 1 = \ kampas 2 = 90 ^ \ circ $.
Tada $ \ trikampis AOB = \ trikampis AOD $ pirmuoju lygybės ženklu.
Taigi $ AB = AD $.
Ir kadangi $ ABCD $ yra lygiagretainis, tai $ BC = AD = AB = CD $, tai yra, $ ABCD $ yra rombas.
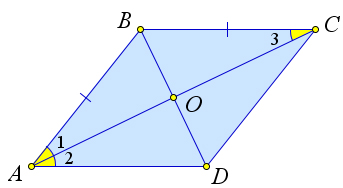
Įrodykime antrąją teoremos dalį.
Apsvarstykite lygiagretainį $ ABCD $, kuriame įstrižainė $ AC $ yra kampo $ \ kampo A $ pusiausvyra, tai yra $ \ kampas 1 = \ kampas 2 $.
Įrodykime, kad $ ABCD $ yra rombas.
$ \ kampas 2 = \ kampas 3 $, kaip kryžminis, todėl $ \ kampas 1 = \ kampas 3 $.
Tai yra, $ \ trikampis ABC $ yra lygiašonis, o $ AB = BC $.
Ir kadangi $ ABCD $ yra lygiagretainis, tai $ AB = CD, BC = AD $, tai yra $ AB = BC = CD = AD $, o $ ABCD $ yra rombas.
Įrodykime trečiąją teoremos dalį
Atkreipkite dėmesį, kad $ \ trikampis ABC = \ trikampis ADC $ antruoju pagrindu ($ \ kampas 1 = \ kampas 2, \ kampas 3 = \ kampas 4 $, $ AC $ yra bendra).
Tada $ \ kampas B = \ kampas D $, todėl jų pusės taip pat yra lygios: $ \ kampas 5 = \ kampas 6 = \ kampas7 = \ kampas 8 $.
Bet tada trikampiai $ \ trikampis ABD $ ir $ \ trikampis BCD $ yra lygiašoniai: $ AB = AD, BC = CD $.
Be to, $ \ trikampis ABD = \ trikampis BCD $ antruoju pagrindu ($ BD $ - iš viso, $ \ kampas 5 = \ kampas6, \ kampas 7 = \ kampas 8 $).
Taigi $ AB = BC $ ir $ AD = CD $.
Taigi visos keturkampio kraštinės yra lygios viena kitai: $ AB = BC = CD = DA $.
Rombas yra keturkampis, kurio kraštinės yra lygios ir poromis lygiagrečios. Skirtingai nuo kvadrato, kurio kampai yra tiesūs, rombas turi du smailius ir du bukus kampus, esančius priešingose pusėse. Tačiau įstrižainės susikerta stačiu kampu ir tuo pačiu yra pusiausvyros. Įstrižainių susikirtimo taškas padalija jas į lygias dalis.
Rombo įstrižainių radimo formulių yra daug, tereikia žinoti pradinius duomenis ir pasirinkti tinkamą.
Kaip rasti rombo įstrižainę per kraštinę ir kampą: kai žinomos rombo kraštinės ir vienas iš kampų, taikomos šios formulės: Per šoninį ir puskampį:
Įstrižainių kvadratų suma lygi kraštinės kvadratui, padaugintam iš keturių D ^ 2 + d ^ 2 = 4a ^ 2. Iš to galime daryti išvadą, kad:
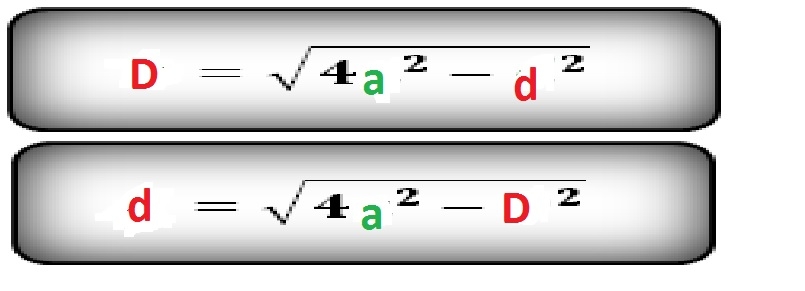

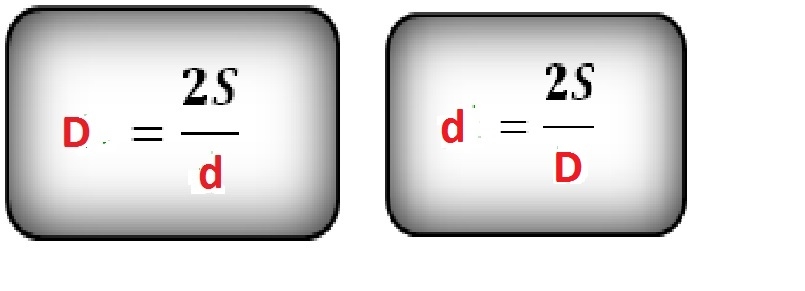
Raskite mažesnę rombo įstrižainę, jei perimetras yra 20 cm, tai didesnė įstrižainė yra 8 cm.
Duota: P = 20cm, D = 8 cm. Raskite vienos rombo kraštinės ilgį, perimetrą padalijus iš keturių a = 20/4 = 5 cm. Naudokime 3 punkto formulę ir gaukime d = (4 * 5 ^ 2-8 ^ 2) ^ 1/2 = 6 cm.
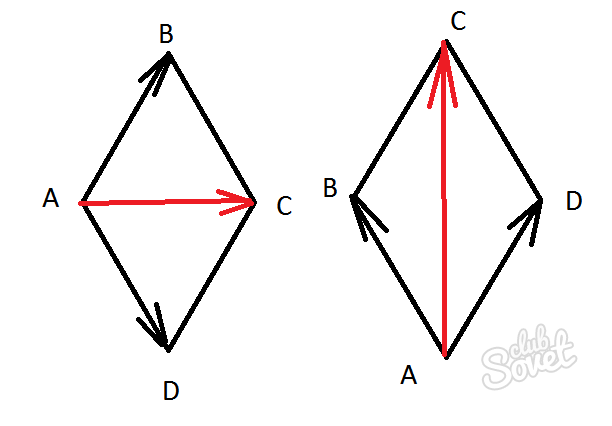
Nepaisant tariamo tokios geometrinės figūros kaip rombo paprastumo, ji kupina daug įdomių akimirkų. Jam taikomos lygiagretainio, pusiaukampio, stačiakampio, o kartais ir lygiašonio trikampio savybės. Žinodami formules galite lengvai išspręsti rombo įstrižainių radimo problemą.
Rombas yra ypatinga geometrijos forma. Dėl ypatingų savybių yra ne viena, o kelios formulės, kuriomis galima apskaičiuoti rombo plotą. Kokios yra šios savybės ir kokios yra dažniausios formulės, leidžiančios rasti šios formos plotą? Išsiaiškinkime.
Kokia geometrinė figūra vadinama rombu
Prieš išsiaiškinant, koks yra rombo plotas, verta išsiaiškinti, kokia tai figūra.
Nuo Euklido geometrijos laikų rombas vadinamas simetrišku keturkampiu, kurio visos keturios kraštinės yra vienodo ilgio ir lygiagrečios poromis.
Termino kilmė
Šios figūros pavadinimas į daugumą šiuolaikinių kalbų atėjo iš graikų, tarpininkaujant lotynų kalbai. Žodžio „rombas“ „protėvis“ buvo graikų kalbos daiktavardis ῥόμβος (tamburinas). Nors dvidešimtojo amžiaus gyventojai, pripratę prie apvalių tambūrų, sunkiai įsivaizduoja kitą jų formą, tačiau tarp graikų tradiciškai šie muzikos instrumentai buvo gaminami ne apvalius, o rombo formos.
Daugumoje šiuolaikinių kalbų vartojamas šis matematinis terminas, kaip ir lotyniškai: rombus. Tačiau į Anglų kalba kartais rombai vadinami deimantu (deimantu arba deimantu). Ši figūra gavo tokį pravardę dėl savo ypatingos formos, primenančios brangus akmuo... Paprastai panašus terminas vartojamas ne visiems rombams, o tik tiems, kurių dviejų kraštinių susikirtimo kampas yra lygus šešiasdešimt ar keturiasdešimt penkių laipsnių.
Ši figūra pirmą kartą paminėta graikų matematiko, gyvenusio pirmame amžiuje, raštuose nauja era- Aleksandrijos herojus.
Kokias savybes turi ši geometrinė figūra?
Norėdami rasti rombo plotą, pirmiausia turite žinoti, kokias savybes jis turi geometrinė figūra. 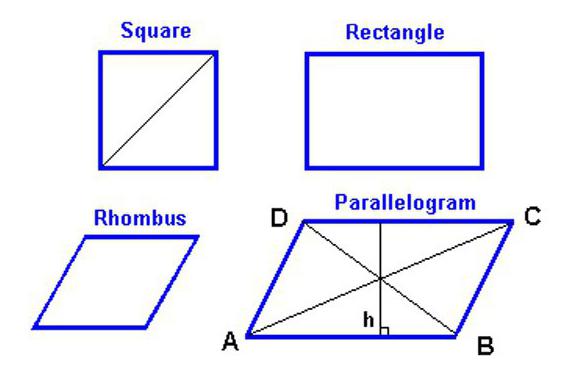
Kokiomis sąlygomis lygiagretainis yra rombas
Kaip žinote, kiekvienas rombas yra lygiagretainis, bet ne kiekvienas lygiagretainis yra rombas. Norint tiksliai teigti, kad pateikta figūra iš tiesų yra rombas, o ne paprastas lygiagretainis, ji turi atitikti vieną iš trijų pagrindinių rombą skiriančių požymių. Arba visus tris iš karto.
- Lygiagretainio įstrižainės susikerta devyniasdešimties laipsnių kampu.
- Įstrižainės padalina kampus į dvi dalis, veikdamos kaip jų pusiausvyros.
- Tokio pat ilgio yra ne tik lygiagrečios, bet ir gretimos kraštinės. Tai, beje, yra vienas iš pagrindinių rombo ir lygiagretainio skirtumų, nes antroji figūra turi tik lygiagrečias vienodo ilgio kraštines, bet ne gretimas.
Kokiomis sąlygomis rombas yra kvadratas
Pagal savo savybes kai kuriais atvejais rombas vienu metu gali tapti kvadratu. Norėdami vizualiai patvirtinti šį teiginį, pakanka tik pasukti kvadratą bet kuria kryptimi keturiasdešimt penkiais laipsniais. Gauta figūra pasirodys kaip rombas, kurio kiekvienas kampas yra lygus devyniasdešimt laipsnių.
Be to, norėdami patvirtinti, kad kvadratas yra rombas, galite palyginti šių figūrų ypatybes: abiem atvejais visos kraštinės yra lygios, o įstrižainės yra pusiausvyros ir susikerta devyniasdešimties laipsnių kampu.
Kaip sužinoti rombo plotą naudojant jo įstrižaines
V modernus pasaulis internete galite rasti beveik visą medžiagą būtiniems skaičiavimams atlikti. Taigi, yra daug išteklių, aprūpintų programomis, skirtomis automatiškai apskaičiuoti tam tikros figūros plotą. Be to, jei (kaip rombo atveju) tam yra kelios formulės, tada yra galimybė pasirinkti, kurią naudoti bus patogiausia. Tačiau, visų pirma, jūs pats turite mokėti be kompiuterio pagalbos apskaičiuoti rombo plotą ir naršyti formules. Rombui jų yra daug, bet žinomiausios iš jų – keturios. 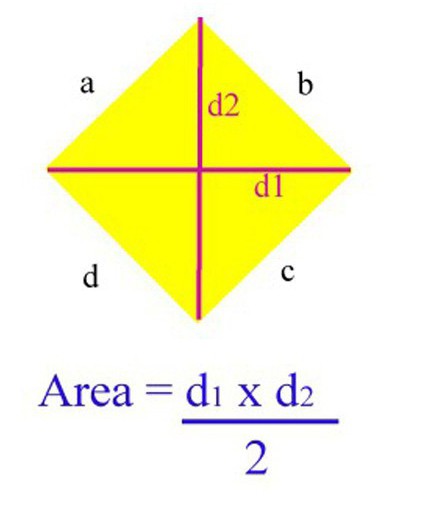
Vienas iš paprasčiausių ir labiausiai paplitusių būdų sužinoti šios figūros plotą, jei yra informacijos apie jos įstrižainių ilgį. Jei užduotyje yra šie duomenys, šiuo atveju galite taikyti šią formulę, kad surastumėte sritį: S = KM x LN / 2 (KM ir LN yra KLMN rombo įstrižainės).
Šios formulės pagrįstumą galite patikrinti praktiškai. Tarkime, kad KLMN rombo vienos įstrižainės KM ilgis yra 10 cm, o antrojo LN - 8 cm. Tada šiuos duomenis pakeičiame aukščiau pateikta formule ir gauname tokį rezultatą: S = 10 x 8/2 = 40 cm2.
Lygiagretainio ploto apskaičiavimo formulė
Taip pat yra kita formulė. Kaip minėta pirmiau rombo apibrėžime, jis yra ne tik keturkampis, bet ir lygiagretainis, ir turi visas šios figūros savybes. Šiuo atveju, norint rasti jo plotą, visai patartina naudoti lygiagretainio formulę: S = KL x Z. Šiuo atveju KL yra lygiagretainio kraštinės ilgis (rombas), o Z yra lygiagretainio kraštinės ilgis. ilgio aukščio, nubrėžto į šią pusę. 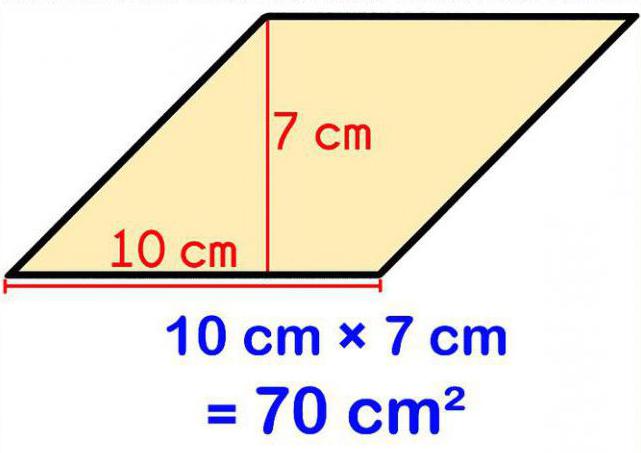
Kai kuriose problemose nenumatytas kraštinės ilgis, bet žinomas rombo perimetras. Kadangi jo suradimo formulė buvo nurodyta aukščiau, galite ją naudoti norėdami sužinoti kraštinės ilgį. Taigi, figūros perimetras yra 10 cm.Kraštinės ilgį galima rasti apvertus perimetro formulę ir 10 padalijus iš 4. Gaunamas 2,5 cm – tai norimas rombo kraštinės ilgis.
Dabar verta pabandyti pakeisti šį skaičių į formulę, žinant, kad į šoną nubrėžto aukščio ilgis taip pat yra 2,5 cm. Dabar pabandykime šias reikšmes įdėti į aukščiau pateiktą lygiagretainio ploto formulę. Pasirodo, rombo plotas yra S = 2,5 x 2,5 = 6,25 cm 2.
Kiti rombo ploto skaičiavimo būdai
Tie, kurie jau yra įvaldę sinusus ir kosinusus, gali naudoti juos turinčias formules, kad surastų rombo plotą. Klasikinis pavyzdys yra tokia formulė: S = KM 2 x Sin KLM. Šiuo atveju figūros plotas yra lygus dviejų rombo kraštinių sandaugai, padaugintam iš kampo tarp jų sinuso. O kadangi rombe visos kraštinės vienodos, tai lengviau iš karto vieną kraštinę pagaminti į kvadratą, kaip parodyta formulėje.
Mes tikriname šią schemą praktiškai ir ne tik iki rombo, bet ir į kvadratą, kuriame, kaip žinote, visi kampai yra teisingi, o tai reiškia, kad jie yra lygūs devyniasdešimt laipsnių. Tarkime, viena iš kraštinių yra 15 cm Taip pat žinoma, kad 90 ° kampo sinusas yra lygus vienetui. Tada pagal formulę S = 15 x 15 x Sin 90 ° = 255x1 = 255 cm 2.
Be to, kas išdėstyta pirmiau, kai kuriais atvejais naudojama kita formulė, naudojant sinusą rombo plotui nustatyti: S = 4 x R 2 / Sin KLM. Šioje versijoje naudojamas rombe įrašytas apskritimo spindulys. Jis pakyla iki kvadrato galios ir padauginamas iš keturių. Ir visas rezultatas yra padalintas iš kampo sinuso, esančio arčiausiai įrašytos figūros.
Kaip pavyzdį, dėl skaičiavimų paprastumo, vėl paimame kvadratą (jo kampo sinusas visada bus lygus vienetui). Jame įrašyto apskritimo spindulys yra 4,4 cm. Tada rombo plotas bus apskaičiuojamas taip: S = 4 x 4,4 2 / Sin 90 ° = 77,44 cm 2
Aukščiau pateiktos rombo spindulio nustatymo formulės toli gražu nėra unikalios, tačiau jas lengviausia suprasti ir atlikti skaičiavimus.
B. A. S. D. Ypatinga rombo savybė. Rombo įstrižainės yra viena kitai statmenos ir per pusę jo kampus. Duota: ABCD rombas. Kadangi rombas yra lygiagretainis, tai BO = DO. Tada AO yra mediana. AO – aukštis. AO yra bisektorius.
11 skaidrė iš pristatymo "Stačiakampių tipai"... Archyvo su pristatymu dydis 275 KB.Geometrija 8 klasė
santrauka kiti pristatymai"" Panašūs trikampiai "8 klasė" - proporcingas vidurkis. Trikampių panašumo ženklai. Panašūs trikampiai. Antrasis ženklas. Kosinusas. О – medianų sankirta. Kasdieniame gyvenime yra tos pačios formos objektų. Užduotis. Stačiojo trikampio kojelė. Segmentai. Vidurinė linija. ASN ir VSN yra stačiakampiai. Medianos trikampyje. Aukštis trikampyje. Stačiojo trikampio smailiojo kampo sinusas. Panašių trikampių apibrėžimas.
„Čevos ir Menelaus teoremos“ – taškai. Chevos teorema. Mokslininko biografija. Menelaus teorema. Taškas K. Chevos ir Menelaus teoremos. Nubrėžkime tiesias linijas. Tiesi linija, lygiagreti pusiausvyrai. Sprendimas. Menelajas iš Aleksandrijos. Taškas. Segmentai. Lygybė. VM-mediana. Vidurinė pusė. Teoremos priešingybė.
"Rasti lygiagretainio plotą" - Raskite lygiagretainio plotą. Lygybės ženklai stačiakampiai trikampiai... Trikampio plotas. Aukštis. Lygiagretainio aukščio nustatymas. Raskite stačiakampio plotą. Teritorijų savybės. Raskite trikampio plotą. Kvadrato plotas. Raskite aikštės plotą. Lygiagretaus plotas. Lygiagretainiai aukščiai. Burnos pratimai. Raskite kvadrato perimetrą. Bazė.
"Apskritimo liestinės konstravimas" - Teorema apie liestinių segmentus. Apskritimas ir tiesė turi vieną bendrą tašką. Kartojimas. Apskritimas. Bendri taškai. Sprendimas. Santykinė tiesės ir apskritimo padėtis. Skersmuo. Apimtis ir tiesi linija. Akordas. Apskritimo liestinė.
"" Apskritimo "geometrija" - teorema apie apskritimą, įrašytą į trikampį. Trikampio pusiausvyros. Apskritimo liestinė. Aplink apskritimą apibrėžto keturkampio kraštinių savybės. Centro statmena teorema. Kampas, kurio viršūnė yra ant apskritimo. Kampo bisektoriaus teorema. Centrinis kampas. Tiesi linija, turinti tik vieną bendrą tašką su apskritimu. Keturkampio, įbrėžto į apskritimą, kampų savybės.
„Pitagoro teoremos sprendimas“ – Hamurabis. Kvadratas. Skersmuo. Kvadrato plotas. Šešiakampiai. Geometrija. Pitagoro teoremos taikymai. Aukštis. Epsteino įrodymas. Trikampiai. Pitagoro biografija. Atimties įrodymas. Visiškas įrodymas. Įrodymas išplėtimo metodu. IX mūsų eros amžiaus įrodymas Motyvas. Pitagoro teorema. Kantoras. Gutheilo įrodymas. Nielseno įrodymas. Teoremos teiginys. pitagoriečiai.
