3 методика:По трем данным сторонамПо двум данным сторонам прямоугольного треугольникаПо двум данным сторонам и углу между ними
Периметр – это общая длина границ двумерной формы. Если вы хотите найти периметр треугольника, то вы должны сложить длины всех его сторон; если вы не знаете длину хотя бы одной стороны треугольника, необходимо найти ее. Эта статья расскажет вам, (а) как найти периметр треугольника по трем известным сторонам; (б) как найти периметр прямоугольного треугольника, когда известны только две стороны; (в) как найти периметр любого треугольника, когда даны две стороны и угол между ними (используя теорему косинусов).
Шаги
Метод 1 из 3: По трем данным сторонам
Метод 2 из 3: По двум данным сторонам прямоугольного треугольника
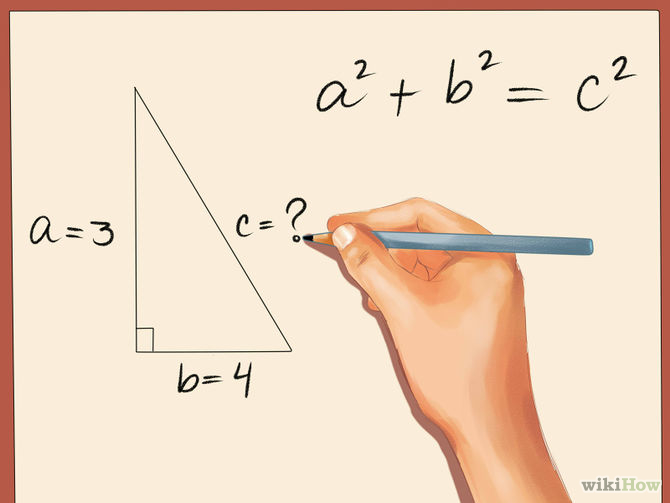
Метод 3 из 3: По двум данным сторонам и углу между ними
- 1 Любую сторону треугольника можно найти по теореме косинусов, если вам даны две стороны и угол между ними. Эта теорема применяется к любым треугольникам и является очень полезной формулой. Теорема косинусов: c2 = a2 + b2 - 2abcos(C), где a, b, c – стороны треугольника, А, B, С – углы, противолежащие соответствующим сторонам треугольника.
- 2
Нарисуйте треугольник и обозначьте стороны как a, b, c; обозначьте противолежащие соответствующим сторонам углы как A, B, C (то есть угол, противолежащий стороне «а», обозначьте как «А» и так далее).
- Например, дан треугольник со сторонами 10 и 12 и углом между ними в 97°, то есть a = 10, b = 12, C = 97°.
- 3
Подставьте данные вам значения в формулу и найдите неизвестную сторону «с».
Сначала возведите в квадрат длины известных сторон и сложите полученные значения. Затем найдите косинус угла С (с помощью калькулятора или онлайн-калькулятора). Умножьте длины известных сторон на косинус данного угла и на 2 (2abcos(C)). Полученное значение вычтите из суммы квадратов двух сторон (a2 + b2), и вы получите c2. Из этой величины извлеките квадратный корень, чтобы найти длину неизвестной стороны «с». В нашем примере:
- c2 = 102 + 122 - 2 × 10 × 12 × cos(97)
- c2 = 100 + 144 – (240 × -0,12187)
- c2 = 244 – (-29,25)
- c2 = 244 + 29,25
- c2 = 273,25
- c = 16,53
- 4
Сложите длины трех сторон, чтобы найти периметр.
Напомним, что периметр вычисляется по формуле: P = a + b + c.
- В нашем примере: Р = 10 + 12 + 16,53 = 38,53.
Периметр треугольника равен сумме длин его сторон:

∠ АОВ + ∠ ВОС = 180° .
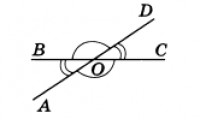
Вертикальные углы равны
Теорема 2.Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1.Угол, смежный с прямым углом, есть прямой угол.

Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 - смежные, углы 1 и 3 - вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
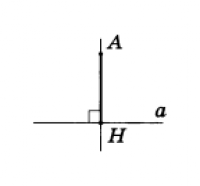
АН - перпендикуляр к прямой
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
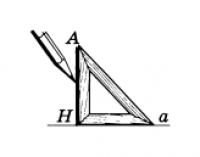
Чертежный угольник
Справедлива следующая теорема.
Четырехзвенная замкнутая ломаная линия - четырехугольник

Трехзвенная замкнутая ломаная линия - треугольник

Плоскость , как и прямая, - это первичное понятие, не имеющее определения. У плоскости, как и у прямой, нельзя видеть ни начала, ни конца. Мы рассматриваем только часть плоскости, которая ограничена замкнутой ломаной линией.
Примером плоскости
является поверхность вашего рабочего стола, тетрадный лист, любая гладкая поверхность. Плоскость можно изобразить как заштрихованную
геометрическую фигуру:
1. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
2 . Через любые две точки можно провести прямую, и только одну.
2.Окружность называется вписанной в треугольник , если она касается всех его сторон. Окружность называется описанной около треугольника , если она проходит через все его вершины. Теорема 1. Центр окружности , вписанной в треугольник , является точкой пересечения его биссектрис.12 окт. 2013 г.
Катет, лежащий против угла 30 градусов
Утверждение
Взаимное расположение двух прямых на плоскости
Cледствия из аксиомы
Следствие1:
Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.
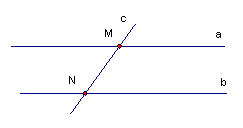
Дано:
![]() .
.
Доказать: .
Доказательство:
Будем доказывать от противного. Предположим, что с не пересекает прямую b (Рис. 4).

Тогда: (по условию), (по предположению). То есть через точку М проходят две прямые (а и c ), параллельные прямой b . А это противоречит аксиоме. Значит, наше предположение неверное. Тогда прямая c пересечет прямую b .
Следствие 2:
Если две прямые параллельны третьей прямой, то они параллельны (Рис. 5).

Дано: .
Доказать: .
Доказательство:
Будем доказывать от противного. Предположим, что прямые a и b пересекаются в некоторой точке М (Рис. 6).

Таким образом, получаем противоречие с аксиомой: через точку М проходят две прямые, одновременно параллельные третьей прямой.
Следовательно, наше предположение неверно. Тогда .
Билет№7
1. У́гол - геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называетсявершиной угла) .
Измерение углов основано на сравнении их с углом, принятым за единицу измерения. Обычно за единицу измерения углов принимают градус - угол, равный 1/180 части развернутого угла.
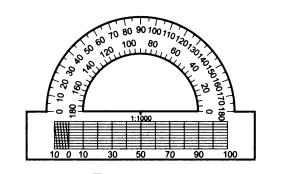
Транспортир
Положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле, называется градусной мерой угла. Для измерения углов используется транспортир (рис.1).

∠AOB = 150°
На рисунке 2 изображен угол АОВ, градусная мера которого равна 150°. Обычно говорят кратко: «Угол АОВ равен 150°» - и пишут: Z АОВ = 150°.
1/60 часть градуса называется минутой, а 1/60 часть минуты - секундой. Минуты обозначают знаком «′», а секунды - знаком «″». Например, угол в 68 градусов, 32 минуты и 27 секунд обозначается так: 68°32′27″.
Если два угла равны, то градус и его части укладываются в этих углах одинаковое число раз, т. е. равные углы имеют равные градусные меры. Если же один угол меньше другого, то в нем градус (или его часть) укладывается меньшее число раз, чем в другом угле, т. е. меньший угол имеет меньшую градусную меру.
Так как градус составляет 1/180: часть развернутого угла, то развернутый угол равен 180°. Неразвернутый угол меньше 180°, так как он меньше развернутого.
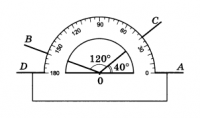
∠AOC = 40°, ∠COB= 120°, ∠AOB = 160°
На рисунке 3 изображены лучи с началом в точке О. Луч ОС делит угол АОВ на два угла: АОС и СОВ. Мы видим, что ∠ АОС = 40°, ∠ СОВ = 120°, ∠ АОВ = 160° .
Таким образом, ∠ АОС + ∠ COB = ∠ АОВ .
Ясно, что и во всех других случаях, когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
Каждый угол имеет определенную градусную меру, больше нуля. Развернутый угол равен 180 градусов.Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом,проходящим между его сторонами
2Второй признак равенства треугольников:
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, такие треугольники равны.
Теорема: Дано . Доказать: АВС и .
Доказательство: Выполним наложение данных в условии фигур. В результате данного действия вершины А и А 1 , , отрезки АС и А 1 С 1 совпадают. Если рассматривать треугольники в целом, то совпадет с .
Теорема доказана.
Билет№8
Билет№9
Билет№10
1.Прямоуго́льный треуго́льник - этотреугольник , в котором один угол прямой (то есть составляет 90 градусов). Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрииНа этом видеоуроке к изучению предлагается тема «Признаки равенства прямоугольных треугольников». В ходе урока вы сможете продолжить разговор о свойствах прямоугольного треугольника. Учитель напомнит признаки равенства обычных треугольников, а затем перейдет к признакам равенства прямоугольных треугольников, которые тесно связаны между собой.
Билет 11.
Билет 12
2 8.4. Построение треугольника по трем сторонам
Построить треугольник с данными сторонами a , b , c .
Построение. С помощью линейки проведем произвольную прямую и отметим на ней произвольную точку B . Раствором циркуля, равным a , описываем окружность с центром в точке B и радиусом a . Пусть C – точка ее пересечения с прямой. Далее описываем окружность с центром в точке B радиуса c и с центром в точке C радиуса b . Пусть A – точка пересечения построенных окружностей. Треугольник ABC – искомый.
Нужно построить треугольник по трем его сторонам при условии, что отрезок a должен принадлежать данному лучу, а один из концов отрезка c должен совпадать с точкой B . Треугольник должен быть отложен от луча в верхнюю полуплоскость.
Билет 13
Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна всем прямым, лежащим в этой плоскости. Признак: Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости. Перпендикуляр к прямой
Что такое перпендикуляр к прямой? Как построить перпендикуляр к прямой? Сколько перпендикуляров можно провести из точки к прямой? Что такое наклонная? Что называется проекцией наклонной? Об этом - ниже.
Определение.
Перпендикуляр, опущенный из точки A на прямую a - это отрезок, лежащий на прямой, перпендикулярной прямой a, один конец которого - точка A, второй - точка пересечения этих двух прямых.
2. Проведём окружность произвольного радиуса с центром в точке А . Получим точкуВ и точку С .
2 С центром в точке В проведем окружность произвольным радиусом. 3 Этим же раствором циркуля проведём окружность с центром в точке С . Получим точку К . 4 Из точки А , через точку К проведём луч. Он будет являться биссектрисой угла А .
Билет 14
1. Треугольник называетсяравнобедренным,
если у него две стороны равны.
Эти равные стороны называются боковыми сторонами
,
а третья сторона называетсяоснованием
треугольника.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Треугольник называется прямоугольным
,
если у него есть прямой угол, то есть угол в 90°.
Сторона прямоугольного треугольника, противолежащая прямому углу, называетсягипотенузой
,
две другие стороны называются катетами
.
Треугольник называется остроугольным, если все три его угла - острые, то есть меньше 90°.
Треугольник называется тупоугольным, если один из его углов - тупой, то есть больше 90°.
2. 8.2. Деление отрезка пополам
Анализ. Пусть [AB ] – данный отрезок, точка O – его середина, прямая a – серединный перпендикуляр к отрезку AB . Выберем произвольную точку C на прямой a , отличную от точки O . В треугольнике ACB CO – одновременно медиана и высота. Следовательно, треугольник ACB равнобедренный, и AC = BC . Отсюда возникает следующий способ построения точки O – середины отрезка AB .
Билет 15.
Билет 16.
2. Теорема 1. В треугольнике против большей стороны лежит больший угол.
Доказательство. Пусть в треугольнике ABC сторона АВ больше стороны АС (рис.1, а).

Докажем, что ∠ С > ∠ В. Отложим на стороне АВ отрезок AD, равный стороне АС (рис.1, б). Так как AD < АВ, то точка D лежит между точками А и В. Следовательно, угол 1 является частью угла С и, значит, ∠ C > ∠ 1. Угол 2 - внешний угол треугольника BDC, поэтому Z 2 > Z В. Углы 1 и 2 равны как углы при основании равнобедренного треугольника ADC. Таким образом, ∠ С > ∠ 1, ∠ 1 = ∠ 2, ∠ 2 > ∠ B. Отсюда следует, что ∠ С > ∠ В.
Справедлива и обратная теорема (ее доказательство проводится методом от противного).
Билет 17
1. Правильный (или равносторонний)треугольник - это правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Все стороны правильноготреугольника равны между собой, все углы также равны и составляют 60°. Вравностороннем треугольнике высота является и биссектрисой, и медианой.
Билет 18
1. Прямоуго́льный треуго́льник - это треугольник, в котором один угол прямой (то есть составляет 90 градусов). Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.
1. Катет- одна из двух сторон, образующих прямой угол в прямоугольном треугольнике.
Гипотенуза (греч. ὑποτείνουσα, натянутая) - самая длинная сторона прямоугольного треугольника, противоположная прямому углу. Длина гипотенузы прямоугольного треугольника может быть найдена с помощью теоремы Пифагора: квадрат длиныгипотенузы равен сумме квадратов длин катетов.
· (Теорема Пифагора)
![]()
· Площадь прямоугольного треугольника равна половине произведения двух его катетов. То есть,
· Для медиан , и выполняется следующее соотношение:
![]()
· В частности, медиана, падающая на гипотенузу, равна половине гипотенузы.
Высота прямоугольного треугольника.
Если высота проведена из вершины с прямым углом к гипотенузе, то треугольник делится на два меньших треугольника, подобных исходному и подобных друг другу. Из этого следует, что в обозначениях, показанных на диаграмме:
· Высота есть среднее геометрическое (среднее пропорциональное) двух образованных ею сегментов гипотенузы, то есть
(иногда это называют теоремой высоты прямоугольного треугольника )
· Каждый катет треугольника есть среднее геометрическое гипотенузы и проекции катета на гипотенузу, то есть
· В прямоугольном треугольнике высота, опущенная из вершины прямого угла на гипотенузу, делит гипотенузу в таком отношении, в каком находятся квадраты прилежащих катетов, то есть
![]()
Кроме того высота, опущенная на гипотенузу, связана с катетами прямоугольного треугольника соотношением:
![]()
Также если прямоугольный треугольник является равнобедренным, то высота, опущенная на гипотенузу будет равна:
2. Построение угла, равного данному
(для демонстрации последовательно нажимайте кнопки с номерами)
| Проведём произвольно луч ЕD . | ||
| С центром в точке В проведем окружность произвольным радиусом. Получим точки M и N . | ||
| Этим же раствором циркуля проведём окружность с центром в точке E . Получим точку К . | ||
| Сделаем раствор циркуля равным расстоянию между точками M и N . | ||
| Не меняя раствора циркуля проводим окружность с центром в точке К . Получим точку F . | ||
| Из точки Е через точку F проведём луч. Получим угол DEF равный углу АВС . |
Билет 19
1. Отрезок прямой - часть прямой, ограниченная двумя точками. Точнее: это множество, состоящее из двух различных точек данной прямой (которые называютсяконцами отрезка ) и всех точек, лежащих между ними (которые называются его внутренними точками). Отрезок, концами которого являются точки и , обозначается символом . Расстояние между концами отрезка называют его длиной и обозначают .
Свойства измерения отрезка:
1.Каждый отрезок имеет определенную длину, большую нуля.
2.Длина отрезка равняется сумме длин частей, на которые он разбивается любой своей внутренней точкой.
3.Расстоянием между двумя точками A и B называется длина отрезка AB .
4.При этом, если точки A и B совпадают, будем считать, что расстояние между ними равно нулю.
5.Два отрезка называются равными, если равны их длины.
1. Угол-часть плоскости между двумя линиями, исходящими из одной точки.
Развернутый угол - это угол, стороны которого составляют прямую (рис. 1).
Градусная мера развернутого угла равна .
Что изучает геометрия?
Геометрия изучает форму предметов, определяет их размеры и взаимное расположение.
Многие предметы имеют прямоугольную форму, другие круглую, третьи - треугольную. Бывают и более сложные формы.
Если посмотреть более внимательно, то можно заметить, что тот же прямоугольник состоит из четырех отрезков, которые образуют его стороны. Т. е. можно сказать, что большинство фигур состоит из более простых фигур. Все фигуры состоят из точек. Поэтому точку можно считать простейшим элементом.
При описании фигур важно ни только указать геометрические примитивы, из которых она состоит, но и "отношения" между ними. Например, прямоугольник не просто состоит из четырех отрезков, но они должны быть соединены между собой; углы, образуемые соединенными отрезками, должны быть прямыми; кроме того отрезки должны быть попарно равны, и отрезки с одинаковой длинной располагаться на противоположных сторонах.
В то же время прямоугольники бывают разными. Один более вытянутый по одной стороне и больше похожий на брусок, у другого ширина и длина не сильно отличаются, и такой прямоугольник похож на квадрат. Ну и понятно, прямоугольники могут различаться по своим размерам. Все это говорит о том, что под термином "прямоугольник" мы понимаем множество фигур, удовлетворяющих определенным требованиям.
Геометрия - древняя наука. Она возникла около 4-5 тыс. лет назад. Людям с древних времен требовалось измерять земельные участки, расстояния, различные предметы, делать замеры при постройке зданий. Слово «геометрия» в переводе с греческого означает «землемерие».
Сначала в истории накапливались правила различных геометрических построений. Потом в Древней Греции появились ученые, которые привнесли в геометрию много нового. В частности начали уделять большую роль рассуждениям, на основе которых можно было открыть новые факты и закономерности. Можно сказать, что геометрия как наука сформировалась к началу нашей эры.
Практическое значение геометрии велико. Кроме того, она учит человека рассуждать, видеть мир форм в их взаимосвязи и взаимодействии.
Наука геометрия делится на два больших раздела - планиметрию и стереометрию. Планиметрия изучает фигуры на плоскости. Это прямоугольники, треугольники, окружности, трапеции, иные четырехугольники. Стереометрия изучает фигуры в трехмерном пространстве. Это шар, куб, цилиндр, пирамида и многие другие.
еометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида.Евклидова геометрия занималась изучением простейших фигур на плоскости и в пространстве, вычислением их площади и объёма. Предложенный Декартом в 1637 году координатный метод лёг в основу аналитической и дифференциальной геометрии, а задачи, связанные с черчением, привели к созданию начертательной и проективной геометрии. При этом все построения оставались в рамкахаксиоматического подхода Евклида. Коренные изменения связаны с работами Лобачевского в 1829 году, который отказался отаксиомы параллельности и создал новую неевклидову геометрию, определив таким образом путь дальнейшего развития науки и создания новых теорий.
Классификация геометрии, предложенная Клейном в «Эрлангенской программе» в 1872 году и содержащая в своей основеинвариантность геометрических объектов относительно различных групп преобразований, сохраняется до сих пор.
Периметр треугольника, формула.
Треугольник это многоугольник с тремя сторонами. Стороны треугольника обозначаются малыми буквами, соответствующими обозначению противоположных вершин.Периметр треугольника равен сумме длин его сторон:
2. Сме́жные углы́ - это пара углов с общей вершиной и одной общей стороной. Две другие стороны составляют продолжение одна другой и образуют прямую линию. Таким образом, вместе смежные углы составляют развёрнутый угол. То есть, величина угла, являющимся смежным для угла величиной α градусов, будет (180 - α) градусов. Смежные и вертикальные углы. Перпендикулярные прямые
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.

Сумма смежных углов равна 180°
Теорема 1.Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.

Вертикальные углы равны
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Треугольник являет собой одну из фундаментальных геометрических фигур, представляющих собой три пересекающихся отрезка прямых. Эта фигура была известна еще ученым Древнего Египта, Древней Греции и Древнего Китая, которые и вывели большинство формул и закономерностей, используемых учеными, инженерами и конструкторами до сих пор.
К основным составным частям треугольника относятся:
Вершины - точки пересечения отрезков.
Стороны - пересекающиеся отрезки прямых.
Исходя из этих составных частей, формулируют такие понятия, как периметр треугольника, его площадь, вписанная и описанная окружность. Еще со школы известно, что периметр треугольника представляет собой числовое выражение суммы всех трех его сторон. В то же время формул для нахождения данной величины известно великое множество, в зависимости от тех исходных данных, которые есть у исследователя в том или ином случае.
1. Самый простой способ нахождения периметра треугольника используется в том случае, когда известны числовые значения всех трех его сторон (x,y,z), как следствие:
2. Периметр равностороннего треугольника можно найти, если вспомнить, что у данной фигуры все стороны, впрочем, как и все углы, равны. Зная длину этой стороны, периметр равностороннего треугольника можно определить по формуле:
3. У равнобедренного треугольника, в отличие от равностороннего, только две боковые стороны имеют одно и то же числовое значение, поэтому в этом случае в общем виде периметр будет находиться следующим образом:
4. Следующие способы необходимы в тех случаях, когда известны числовые значения не всех сторон. Например, если в исследовании есть данные о двух сторонах, а также известен угол между ними, то периметр треугольника может быть найден с помощью определения третьей стороны и известного угла. В этом случае эта третья сторона будет найдена по формуле:
z= 2x+2y-2xycosβ
Исходя из этого, периметр треугольника будет равен:
P= x+y+2x+(2y-2xycos β)
5. В том случае, когда изначально дана длина не более чем одной стороны треугольника и известны числовые величины двух углов прилегающих к ней, то периметр треугольника можно вычислить, опираясь на теорему синусов:
P = x+sinβ х/(sin(180°-β)) + sinγ x/(sin(180°-γ))
6. Бывают случаи, когда для нахождения периметра треугольника используются известные параметры вписанной в него окружности. Данная формула также известна большинству еще со школьной скамьи:
P= 2S/r (S - площадь окружности, тогда как r - ее радиус).
Из всего вышеприведенного видно, что величина периметра треугольника может быть найдена множеством способов, исходя из тех данных, которыми владеет исследователь. Кроме того, есть еще несколько частных случаев нахождения данной величины. Так, периметр является одной из важнейших величин и характеристик прямоугольного треугольника.
Как известно, таким треугольником называют фигуру, две стороны которой образуют прямой угол. Периметр прямоугольного треугольника находится через числовое выражение суммы обоих катетов и гипотенузы. В том случае, если исследователю известны данные только о двух сторонах, оставшуюся можно вычислить с помощью знаменитой теоремы Пифагора: z= (x2 + y2), если известны оба катета, или x= (z2 - y2), если известна гипотенуза и катет.
В том случае, если известна длина гипотенузы и один из прилежащих у ней углов, то две другие стороны находятся по формулам: х= z sinβ , y= z cosβ. В этом случае периметр будет равен:
P= z(cosβ + sinβ +1)
Также частным случаем является вычисление периметра правильного (или равностороннего) треугольника, то есть такой фигуры, у которой все стороны и все углы равны. Вычисление периметра такого треугольника по известной стороне никакой проблемы не составляет, однако, зачастую исследователю известны какие-то другие данные. Так, если известен радиус вписанной окружности, периметр правильного треугольника находится по формуле:
А если дана величина радиуса описанной окружности, периметр правильного треугольника будет найден следующим образом:
Формулы нужно запомнить, чтобы успешно применть на практике.
