Ситуационен модел хищник-плячка
Нека разгледаме математически модел на динамиката на съвместното съществуване на два биологични вида (популации), взаимодействащи помежду си според типа "хищник-плячка" (вълци и зайци, щуки и караси и др.), наречен Volter-Lotka модел. За първи път е получен от А. Лотка (1925), а малко по-късно и независимо от Лотка, подобни и по-сложни модели са разработени от италианския математик В. Волтера (1926), чиято работа всъщност поставя основите на т.нар. математическа екология.
Нека има два биологични вида, които живеят заедно в изолирана среда. Това предполага:
- 1. Жертвата може да намери достатъчно храна за хранене;
- 2. При всяка среща на плячката с хищника, последният убива жертвата.
За яснота ще ги наречем караси и щуки. Позволявам
състоянието на системата се определя от количествата x (t)и y (t)- броят на караси и щуки наведнъж г.За да получим математически уравнения, които приблизително описват динамиката (промяната във времето) на популацията, ще продължим както следва.
Както в предишния модел на нарастване на населението (вижте раздел 1.1), за жертвите имаме уравнението
където а> 0 (плодовитостта надвишава смъртността)
Коефициент арастежът на плячката зависи от броя на хищниците (намалява с увеличаването им). В най-простия случай a - a - fjy (a> 0, p> 0).Тогава за размера на популацията жертви имаме диференциалното уравнение
За популацията от хищници имаме уравнението

където б> 0 (смъртността надвишава раждаемостта).
Коефициент бнамаляването на хищниците намалява, ако има плячка за ядене. В най-простия случай можете да вземете b - y -Sx (y > 0, С> 0). Тогава за размера на популацията от хищници получаваме диференциалното уравнение

По този начин уравненията (1.5) и (1.6) представляват математически модел на разглеждания проблем за взаимодействието между популациите. В този модел променливите x, y- състоянието на системата, а коефициентите характеризират нейната структура. Нелинейната система (1.5), (1.6) е моделът на Волтер-Лотка.
Уравненията (1.5) и (1.6) трябва да бъдат допълнени с начални условия - дадени стойности на началните популации.
Нека сега анализираме построения математически модел.
Нека построим фазовия портрет на системата (1.5), (1.6) (в смисъла на задачата х> 0, v > 0). Разделяйки уравнение (1.5) на уравнение (1.6), получаваме уравнение с разделими променливи
Като пренебрегнем това уравнение, имаме
Съотношение (1.7) дава уравнението на фазовите траектории в имплицитна форма. Системата (1.5), (1.6) има стационарно състояние, определено от

От уравнения (1.8) получаваме (тъй като l * Ф 0, y * Ф 0)
Равенствата (1.9) определят положението на равновесие (т о)(фиг. 1.6).

От тези съображения може да се определи посоката на движение по фазовата траектория. Нека шараните са малко. G. e. x ~ 0, то от уравнение (1.6) y
Всички фазови траектории (с изключение на точката 0) затворени криви, покриващи положението на равновесие. Състоянието на равновесие съответства на постоянно число x "и y" на караси и щуки. Карасите се размножават, щуките ги ядат, умират, но броят на тези и другите не се променя. „Затворените фазови траектории съответстват на периодична промяна в броя на караси и щуки. Освен това траекторията, по която се движи фазовата точка, зависи от началните условия. Помислете как се променя състоянието по фазовата траектория. Нека точката е в позицията А(фиг. 1.6). Има малко караси, много щуки; щуките нямат какво да ядат и постепенно измират и почти
изчезват напълно. Но броят на карасите също намалява до почти нула и
едва по-късно, когато щуката стана по-малко от в, започва увеличаването на броя на карасите; темпът на растежа им се увеличава и броят им се увеличава - това се случва до около точка V.Но увеличаването на броя на карасите води до инхибиране на процеса на изчезване на шук и техният брой започва да расте (има повече храна) - сайтът слънце.Тогава има много щуки, те ядат караси и ядат почти всички (сайт CD).След това щуките отново започват да измират и процесът се повтаря с период от около 5-7 години. На фиг. 1.7 качествено начертани криви на промените в броя на караси и щуки в зависимост от времето. Редуват се максимумите на кривите, като максимумите на изобилието на щуки изостават от максимумите на караси.

Това поведение е типично за различни системи от типа хищник-плячка. Нека сега интерпретираме получените резултати.
Въпреки факта, че разглежданият модел е най-простият и в действителност всичко е много по-сложно, той даде възможност да се обяснят някои от мистериозните, които съществуват в природата. Разбираеми са разказите на рибарите за периодите, когато „самите щуки им скачат в ръцете“;
Обърнете внимание на още един интересен извод, който може да се направи от фиг. 1.6. Ако в точката Рима бърз улов на щуки (в друга терминология - стрелба по вълци), след което системата "скача" до точката Q,и по-нататъшното движение се осъществява по затворена траектория с по-малък размер, което интуитивно се очаква. Ако намалим броя на щуките в точката R,тогава системата ще отиде в точката С,и по-нататъшното движение ще следва по-голяма траектория. Амплитудите на вибрациите ще се увеличат. Това противоречи на интуицията, но просто обяснява това явление: в резултат на отстрела на вълци броят им се увеличава с времето. По този начин изборът на момента на стрелба е важен в случая.
Да предположим, че две популации от насекоми (например листна въшка и калинка, която е листна въшка) са в естествено равновесие x-x *, y = y *(точка Она фиг. 1.6). Помислете за въздействието на еднократно приложение на инсектицид, който убива x> 0 от пострадалите и y> 0 от хищниците, без да ги унищожи напълно. Намаляването на броя и на двете популации води до факта, че представителната точка от позицията ОЩе "скочи" по-близо до произхода, където x> 0, y 0 (фиг. 1.6) От това следва, че в резултат на действието на инсектицида, предназначен да унищожи жертвите (листни въшки), броят на жертвите (листни въшки) се увеличава, а броят на хищниците (калинките) намалява. Оказва се, че броят на хищниците може да стане толкова малък, че те ще обичат пълното изчезване, но по други причини (суша, болест и др.). По този начин използването на инсектициди (освен ако не унищожават почти напълно вредните насекоми) в крайна сметка води до увеличаване на популацията на тези насекоми, чийто брой е бил под контрола на други хищни насекоми. Такива случаи са описани в книги по биология.
В общия случай темпът на нарастване на броя на жертвите азависи както от L ", така и от y: а= a (x, y) (поради наличието на хищници и поради хранителни ограничения).
С малка промяна в модела (1.5), (1.6), малки членове се добавят към дясната страна на уравненията (като се вземе предвид например конкуренцията на шаран за храна и щука за шаран)
тук 0 f.i «1.
В този случай изводът за периодичността на процеса (връщането на системата в първоначалното й състояние), който е валиден за модела (1.5), (1.6), губи своята валидност. В зависимост от вида на малките корекции / и жситуациите, показани на фиг. 1.8.

В случай (1) равновесното състояние Остабилен. При всякакви други начални условия именно това се установява след достатъчно дълго време.
В случай (2) системата е "изчерпана". Стационарното състояние е нестабилно. Такава система в крайна сметка попада в такъв диапазон от стойности хи y, че моделът вече не е приложим.
В случай (3) в система с нестабилно стационарно състояние Овъв времето се установява периодичен режим. За разлика от оригиналния модел (1.5), (1.6), в този модел стационарният периодичен режим не зависи от началните условия. Първоначално малко отклонение от стационарното състояние Оводи до не малки колебания около О, както при модела на Волтера-Лотка, но да осцилира напълно определена (и не зависима от малкото отклонение) амплитуда.
В И. Арнолд нарича модела Волтера-Лотка твърд, т.к малката му промяна може да доведе до изводи, различни от посочените по-горе. За да прецените коя от ситуациите, посочени на фиг. 1.8, е внедрен в тази система, допълнителна информация за системата е абсолютно необходима (относно формата на малки корекции / и ж).
Модели на взаимодействие от два вида
Хипотезите на Волтера. Аналогии с химическата кинетика. Volterra модели на взаимодействия. Класификация на видовете взаимодействия Конкуренция. Хищник-плячка. Обобщени модели на взаимодействие на възгледите . Моделът на Колмогоров. Модел на взаимодействие на два вида насекоми Макартур. Параметрични и фазови портрети на системата Базикин.
Основателят на съвременната математическа теория на популациите с право се счита италианският математик Вито Волтера, който разработи математическата теория на биологичните общности, чийто апарат са диференциални и интегро-диференциални уравнения.(Вито Волтера. Lecons sur la Theorie Mathematique de la Lutte pour la Vie. Paris., 1931). През следващите десетилетия динамиката на населението се развива главно в съответствие с идеите, изразени в тази книга. Руският превод на книгата на Волтера е публикуван през 1976 г. под заглавието: „Математическата теория на борбата за съществуване“ с послеслов от Ю.М. Свирежев, който разглежда историята на развитието на математическата екология в периода 1931-1976 г.
Книгата на Волтера е написана по начина, по който се пишат книгите по математика. Първо се формулират някои предположения за математическите обекти, които се предполага, че се изучават, а след това се извършва математическо изследване на свойствата на тези обекти.
Системите, изследвани от Volterra, се състоят от два или повече типа. В някои случаи се взема предвид доставката на използвана храна. Уравненията, описващи взаимодействието на тези типове, се основават на следните представяния.
Хипотезите на Волтера
1. Храната или се предлага в неограничени количества, или приемът й във времето е строго регламентиран.
2. Индивидите от всеки вид умират, така че постоянна част от съществуващите индивиди загиват за единица време.
3. Хищните видове изяждат плячката си, като за единица време броят на изядената плячка винаги е пропорционален на вероятността за среща на индивиди от тези два вида, т.е. произведението на броя на хищниците към броя на жертвите.
4. Ако храната е налична в ограничени количества и няколко вида са способни да я консумират, то делът на храната, консумирана от даден вид за единица време, е пропорционален на броя на индивидите от този вид, взети с определен коефициент в зависимост от видове (модел на междувидова конкуренция).
5. Ако даден вид се храни с храна, налична в неограничени количества, увеличаването на броя на видовете за единица време е пропорционално на броя на вида.
6. Ако един вид се храни с храна, която е налична в ограничени количества, то размножаването му се регулира от скоростта на консумация на храна, т.е. за единица време увеличението е пропорционално на количеството изядена храна.
Аналогии с химическата кинетика
Тези хипотези имат близки паралели с химическата кинетика. В уравненията на динамиката на населението, както и в уравненията на химическата кинетика, се използва „принципът на сблъсъците“, когато скоростта на реакцията е пропорционална на произведението на концентрациите на реагиращите компоненти.
Всъщност, според хипотезите на Волтера, скоросттапроцес умирането на всеки вид е пропорционално на броя на видовете. В химичната кинетика това съответства на мономолекулна реакция на разлагане на някакво вещество, а в математическия модел - на отрицателни линейни членове от дясната страна на уравненията.
Според концепциите на химическата кинетика скоростта на бимолекулната реакция на взаимодействието на две вещества е пропорционална на вероятността от сблъсък на тези вещества, т.е. продуктът на тяхната концентрация. По същия начин, в съответствие с хипотезите на Волтера, скоростта на възпроизвеждане на хищници (смърт на плячка) е пропорционална на вероятността от срещи между индивиди на хищник и плячка, т.е. произведението на техните числа. И в двата случая билинейните членове се появяват в моделната система от дясната страна на съответните уравнения.
И накрая, линейните положителни членове от дясната страна на уравненията на Волтера, съответстващи на растежа на популациите при неограничени условия, съответстват на автокаталитичните членове на химичните реакции. Това сходство на уравненията в химичните и екологичните модели дава възможност да се прилагат същите изследователски методи за математическо моделиране на кинетиката на популациите, както при системите от химични реакции.
Класификация на видовете взаимодействия
В съответствие с хипотезите на Волтера, взаимодействието на два вида, чиито числа х 1 и х 2 може да се опише с уравненията:
(9.1)
Ето параметрите а и - константи на собствения темп на растеж на вида, ° С аз - константи на самоограничаване на броя (вътрешновидова конкуренция), b ij- константи на взаимодействие на видовете, (и, j = 1,2). Знаците на тези коефициенти определят вида на взаимодействието.
В биологичната литература взаимодействията обикновено се класифицират според включените механизми. Разнообразието тук е огромно: различни трофични взаимодействия, химични взаимодействия, които съществуват между бактерии и планктонни водорасли, взаимодействия на гъбички с други организми, поредици от растителни организми, свързани по-специално с конкуренция за слънчева светлина и с еволюцията на почвите и др. Тази класификация изглежда огромна.
Е ... Одум, като взе предвид моделите, предложени от В. Волтера, предложи класификация не по механизми, а по резултати. Според тази класификация връзката трябва да се оценява като положителна, отрицателна или неутрална в зависимост от това дали броят на един вид се увеличава, намалява или остава непроменен в присъствието на друг вид. Тогава основните видове взаимодействия могат да бъдат представени под формата на таблица.
ВИДОВЕ ВЗАИМОДЕЙСТВИЕ НА ВИДОВЕ
|
СИМБИОЗА |
б 12 ,б 21 >0 |
||
|
КОМЕНСАЛИЗЪМ |
б 12 ,>0, б 21 =0 |
||
|
ЖЕРТВА НА ХИЩНИК |
б 12 ,>0, б 21 <0 |
||
|
АМЕНСАЛИЗЪМ |
б 12 ,=0, б 21 <0 |
||
|
КОНКУРЕНЦИЯ |
б 12 , б 21 <0 |
||
|
НЕУТРАЛИЗЪМ |
б 12 , б 21 =0 |
Последната колона показва знаците на коефициентите на взаимодействие от система (9.1)
Нека разгледаме основните видове взаимодействия
КОНКУРЕНЦИЯ Уравнения:
Както видяхме в Лекция 6, уравненията на конкуренцията са:
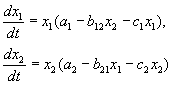 (9.2)
(9.2)
Стационарни системни решения:
(1).
![]()
Произходът на координатите за всички параметри на системата е нестабилен възел.
(2).
![]() (9.3)
(9.3)
° С стационарното състояние (9.3) е седло при а 1 > б 12 /С 2 и
стабилен възел при а 1 12 / с 2 . Това условие означава, че видът умира, ако неговият собствен растеж е по-малък от определена критична стойност.
(3).
![]() (9.4)
(9.4)
° С стационарно решение (9.4)¾ седло при а 2 > б 21 / ° С 1 и стабилен възел при а 2< б 21 / ° С 1
(4).
![]() (9.5)
(9.5)
Стационарното състояние (9.5) характеризира съвместното съществуване на два конкуриращи се вида и е стабилен възел, ако е изпълнено отношението:
![]()
Следователно неравенството следва:
б 12
б 21
което позволява да се формулира условието за съвместно съществуване на видовете:
Продуктът на коефициентите на взаимодействие между популациите е по-малък от произведението на коефициентите в рамките на взаимодействието на популацията.
Наистина, нека естествените темпове на растеж на двата разглеждани видаа 1 , а 2 са същите. Тогава необходимото условие за стабилност ще бъде
° С 2 > б 12 , ° С 1 > б 21 .
Тези неравенства показват, че увеличаването на броя на един от конкурентите потиска собствения му растеж повече от растежа на друг конкурент. Ако изобилието и на двата вида е ограничено, частично или изцяло, от различни ресурси, горните неравенства са валидни. Ако и двата вида имат абсолютно еднакви нужди, тогава един от тях ще бъде по-жизнеспособен и ще измести своя конкурент.
Поведението на фазовите траектории на системата осигурява визуално представяне на възможните резултати от конкуренцията. Нека приравним към нула десните страни на уравненията на системата (9.2):
х 1 (а 1 –в 1 х 1 – б 12 х 2) = 0 (dx 1 /dt = 0),
х 2 (а 2 –б 21 х 1 – ° С 2 х 2) = 0 (dx 2 /dt = 0),
В този случай получаваме уравнения за главните изоклини на системата
х 2 = - b 21 х 1 / ° С 2 +а 2 / c 2, х 2 = 0
- уравнения на изоклини на вертикални допирателни.
х 2 = - c 1 х 1 / b 12 + а 1 / б 12 , х 1 = 0
- уравнения на изоклини на вертикални допирателни. Точките на пресичане по двойки на изоклини на вертикални и хоризонтални допирателни системи са стационарни решения на системата от уравнения (9.2.) и техните координати ![]() са стационарните числа на конкуриращите се видове.
са стационарните числа на конкуриращите се видове.
Възможното разположение на главните изоклини в системата (9.2) е показано на фиг. 9.1. Ориз. 9.1асъответства на оцеляването на видах 1, фиг. 9.1 б- оцеляване на видах 2, фиг. 9.1 v- съвместното съществуване на видове при условие (9.6). Фигура 9.1гдемонстрира тригерна система. Тук резултатът от състезанието зависи от първоначалните условия. Стационарното състояние (9.5), което е различно от нула и за двата типа, е нестабилно. Това е седлото, през което преминава сепаратрисата, разделяйки зоните за оцеляване на всеки вид.

Ориз. 9.1.Разположението на главните изоклини във фазовия портрет на състезателната система Volterra от два типа (9.2) с различни съотношения на параметрите. Обяснения в текста.
За изследване на конкуренцията между видовете бяха проведени експерименти върху голямо разнообразие от организми. Обикновено два тясно свързани вида се избират и отглеждат заедно и поотделно при строго контролирани условия. На редовни интервали се извършва пълно или селективно преброяване на популацията. Запишете данни от няколко повторения и анализирайте. Проведени са проучвания върху протозои (по-специално реснички), много видове бръмбари от рода Tribolium, плодови мухи, сладководни ракообразни (дафнии). Извършени са много експерименти върху микробни популации (вж. Лекция 11). Експерименти са правени и в природата, включително броя на планарията (Reynolds), два вида мравки (Pontinus) и др. 9.2. показва кривите на растеж на диатомеите, използващи същия ресурс (заемащи същата екологична ниша). Когато се отглежда в монокултураАстерионела Формоза достига постоянно ниво на плътност и поддържа концентрацията на ресурса (силиката) на постоянно ниско ниво. Б. Когато се отглежда в монокултураСинедрауина се държи по подобен начин и поддържа концентрацията на силикат на още по-ниско ниво. Б. При съвместно култивиране (в два екземпляра) Synedrauina замества Asterionella Formosa. Явно Синедра

Ориз. 9.2.Състезание между диатомеите. а -когато се отглежда в монокултураАстерионела Формоза достига постоянно ниво на плътност и поддържа концентрацията на ресурса (силиката) на постоянно ниско ниво. б -когато се отглежда в монокултураСинедрауина се държи по подобен начин и поддържа концентрацията на силикат на още по-ниско ниво. v -в съвместно култивиране (в два екземпляра) Synedruina замества Asterionella Formosa. Явно Синедра печели конкуренцията поради способността си да използва по-пълно субстрата (вижте също Лекция 11).
Широко известни са експериментите по изследване на конкуренцията на Г. Гаузе, които демонстрират оцеляването на един от конкуриращите се видове и му позволяват да формулира „закона на конкурентното изключване“. Законът гласи, че само един вид може да съществува в една екологична ниша. На фиг. 9.3. показва резултатите от експериментите на Гаузе за два вида Parametium, заемащи една екологична ниша (фиг. 9.3 а, б) и видове, заемащи различни екологични ниши (фиг. 9.3. в).

Ориз. 9.3. а- Криви на прираст на популацията на два видаПараметий в едновидови култури. черни кръгове - P Аурелия, бели кръгове - P. Каудатум
б- Криви на растеж на P Aurelia и P. Каудатум в смесена култура.
От Гаузе, 1934 г
Моделът на конкуренцията (9.2) има недостатъци, по-специално от него следва, че съвместното съществуване на два вида е възможно само ако броят им е ограничен от различни фактори, но моделът не дава индикация колко големи трябва да бъдат разликите за гарантират дългосрочно съжителство. В същото време е известно, че за дългосрочно съжителство в променлива среда е необходима разлика, която достига определена стойност. Въвеждането на стохастични елементи в модела (например въвеждането на функция за използване на ресурси) позволява количествено да се изследват тези въпроси.
Система ХИЩНИК + ЖЕРТВА
 (9.7)
(9.7)
Тук, за разлика от (9.2), знаците б 12 и б 21 са различни. Както при конкуренцията, произходът е
![]() (9.8)
(9.8)
е единична точка от типа нестабилен възел. Три други възможни стационарни състояния:
![]() ,(9.9)
,(9.9)
![]() (9.10)
(9.10)
![]() (9.11)
(9.11)
По този начин е възможно да оцелее само плячката (9.10), само хищникът (9.9) (ако има други източници на храна) и съвместното съществуване на двата вида (9.11). Последният вариант вече беше разгледан от нас в Лекция 5. Възможните типове фазови портрети за системата хищник-плячка са показани на фиг. 9.4.
Изоклините на хоризонталните допирателни са прави линии
х 2 = – б 21 х 1 /° С 2 + а 1 / c 2, х 2 = 0,
и изоклини на вертикални допирателни- права
х 2 = - ° С 1 х 1 /б 12 + а 2 /б 12 , х 1 = 0.
Стационарните точки лежат в пресечната точка на изоклините на вертикални и хоризонтални допирателни.

От фиг. 9.4 се вижда следното. Система хищник-плячка (9.7) може да има стабилно равновесно положение, в коткатао ром населението на жертвите е напълно изчезнало ( ) и останаха само хищниците (точка 2 на фиг. 9.4 а). Очевидно такава ситуация може да се реализира само ако освен разглеждания тип жертви х 1 хищник х 2 - има допълнителни захранвания. Този факт е отразен в модела чрез положителен член от дясната страна на уравнението за x 2. Специални точки(1) и (3) (фиг.9.4 а) са нестабилни. Втора възможност – стационарно стационарно състояние, при което популацията на хищниците е напълно изчезнала и е останала само плячка – стабилна точка(3) (фиг.9.4 6 ). Ето една специална точка (1) – също нестабилен възел.
И накрая, третата възможност – стабилно съвместно съществуване на популации от хищник и плячка (фиг. 9.4 v), чиито стационарни числа се изразяват с формулите (9.11).
Както в случая с една популация (вж. Лекция 3), за модела (9.7) можете да разработите стохастичен модел, но не можете да получите изрично решение за него. Затова ще се ограничим до общи съображения. Да предположим, например, че равновесната точка е на известно разстояние от всяка от осите. След това, за фазови траектории, на които стойноститех 1 , х 2 остават достатъчно големи, детерминиран модел ще бъде доста задоволителен. Но ако в даден момент от фазовата траектория някоя променлива не е много голяма, тогава произволните флуктуации могат да придобият значително значение. Те водят до факта, че изобразяващата точка ще се премести към една от осите, което означава изчезване на съответния вид.
По този начин стохастичният модел се оказва нестабилен, тъй като стохастичният „дрифт“ рано или късно води до изчезване на един от видовете. В този вид модел хищникът в крайна сметка умира, това може да се случи или случайно, или поради факта, че популацията на плячката му първо се елиминира. Стохастичният модел на системата хищник - плячка обяснява добре експериментите на Гаузе (Gause, 1934), в който ресничките Paramettum candatumпослужил като жертва на друга ресничка Didinium nasatum – хищник. Очаква се според детерминираните уравнения (9.7) равновесното изобилие в тези експерименти е приблизително само пет индивида от всеки вид, така че няма нищо изненадващо във факта, че при всеки повторен експеримент или хищници, или плячка (а след тях и хищници) умират доста бързо. Резултатите от експериментите са представени на фиг. 9.5.

Ориз. 9.5. Растеж Parametium caudatum и хищни реснички Dadinium nasutum. От : Gause G.F. Борбата за съществуване. Балтимор, 1934
И така, анализът на моделите на Volterra за взаимодействие между видовете показва, че въпреки голямото разнообразие от видове поведение на такива системи, изобщо не може да има непрекъснати колебания в броя на конкуриращите се видове в модела. В природата и в експеримента обаче се наблюдават такива колебания. Необходимостта от тяхното теоретично обяснение беше една от причините за формулирането на описания на моделите в по-общ вид.
Обобщени модели на взаимодействие от два типа
Предложени са голям брой модели, които описват взаимодействието на видовете, десните страни на уравненията на които са функции на броя на взаимодействащите популации. Въпросът за разработването на общи критерии беше решен, за да се установи какви функции могат да опишат характеристиките на поведението на временния размер на населението, включително стабилни флуктуации. Най-известните от тези модели принадлежат на Колмогоров (1935, преработена статия - 1972) и Розенцвайг (1963).
 (9.12)
(9.12)
Моделът се основава на следните допускания:
1) Хищниците не взаимодействат помежду си, т.е. скорост на размножаване на хищници к 2 и броя на жертвите Л, унищожен за единица време от един хищник, не зависи от г.
2) Увеличаването на броя на жертвите в присъствието на хищници е равно на увеличаването на отсъствието на хищници минус броя на жертвите, унищожени от хищниците. Функции к 1 (х), к 2 (х), Л(х), са непрекъснати и дефинирани върху положителната полуос х, г³ 0.
3) дк 1 / dx< 0. Това означава, че скоростта на възпроизвеждане на плячка при отсъствие на хищник намалява монотонно с увеличаване на броя на плячката, което отразява ограничените хранителни и други ресурси.
4) дк 2 / dx> 0, к 2 (0) < 0 < k 2 (¥ ). С увеличаване на броя на плячката, репродуктивната скорост на хищниците монотонно намалява с увеличаване на броя на плячката, преминавайки от отрицателни стойности (когато няма какво да се яде) към положителни.
5) Броят на жертвите, унищожени от един хищник за единица време Л(х)> 0 в N> 0; Л(0)=0.
Възможните типове фазови портрети на системата (9.12) са показани на фиг. 9.6:

Ориз. 9.6.Фазови портрети на системата на Колмогоров (9.12), описващи взаимодействието на два типа при различни съотношения на параметрите. Обяснения в текста.
Стационарните решения (има две или три) имат следните координати:
(1). ` х = 0;` y = 0.
Началото на координатите за всякакви стойности на параметрите е седло (фиг. 9.6 a-d).
(2). ` x = A,` y = 0.(9.13)
Асе определя от уравнението:
к 1 (А)=0.
Стационарен решение (9.13) е седло, ако Б< А (фиг.9.6 а, б, г), Б се определя от уравнението
к 2 (Б)=0
Точка (9.13) се поставя в положителния квадрант, ако B> А . Това е стабилен възел .
Последният случай, който съответства на смъртта на хищника и оцеляването на плячката, е показан на фиг. 9.6 v.
(3). ` x = B,` y = C.(9.14)
Стойността на C се определя от уравненията:
Точка (9.14) - фокус (фиг. 9.6 а) или възел (фиг. 9.6 г), чиято стабилност зависи от знака на количествотос
с 2 = – к 1 (Б) - к 1 (Б)B + L(Б)° С.
Ако с>0, точката е стабилна, акос<0 ‑ точка неустойчива, и вокруг нее могут существовать предельные циклы (рис. 9.6 б)
В чуждестранната литература често се разглежда подобен модел, предложен от Розенцвайг и Макартур (1963):
 (9.15)
(9.15)
където е(х) е скоростта на промяна в броя на жертвите хпри липса на хищници, Ф ( x, y) е интензивността на хищничеството, к- коефициент, характеризиращ ефективността на превръщането на биомасата на плячка в биомаса на хищник, д- смъртност на хищниците.
Моделът (9.15) се свежда до частен случай на модела на Колмогоров (9.12) при следните допускания:
1) броят на хищника е ограничен само от броя на плячката,
2) скоростта, с която даден хищник изяжда плячка зависи само от плътността на популацията на плячката и не зависи от плътността на популацията на хищника.
Тогава уравненията (9.15) приемат формата.

Когато се описва взаимодействието на реални видове, десните страни на уравненията се конкретизират в съответствие с представите за биологичните реалности. Помислете за един от най-популярните модели от този тип.
Модел на взаимодействие на два вида насекоми (М акАртър, 1971)
Моделът, който ще разгледаме по-долу, беше използван за решаване на практическия проблем за борба с вредните насекоми чрез стерилизиране на мъжки от един от видовете. Въз основа на биологичните характеристики на взаимодействието на видовете е написан следният модел
 (9.16)
(9.16)
Тук x, y- биомаса на два вида насекоми. Трофичните взаимодействия на видовете, описани в този модел, са много сложни. Това определя формата на полиномите от дясната страна на уравненията.
Разгледайте дясната страна на първото уравнение. Видове насекоми хядат ларви от вида в(член + k 3 y),но възрастните от вида вядат ларви от вида хобект на голям брой видове хили вили и двете (членове - к 4 xy, - y 2). За малки хсмъртност на вида хпо-висок от естествения му прираст (1 –К 1 + k 2 х – х 2 < 0 при малки Х).Във второто уравнение членът к 5 отразява естествения растеж на вида y; –К 6 y -самоограничение от този вид,–К 7 х- ядене на ларви от вида ввидове насекоми х, к 8 xy – увеличаване на биомасата на видовете впоради изяждане от възрастни насекоми от вида вларви на вида Х.
На фиг. 9.7 е представен пределният цикъл, който е траекторията на устойчиво периодично решение на системата (9.16).

Решението на въпроса как да се осигури съвместното съществуване на една популация с нейната биологична среда, разбира се, не може да се получи без отчитане на спецификата на определена биологична система и анализ на всички нейни взаимовръзки. В същото време изучаването на формалните математически модели ни позволява да отговорим на някои общи въпроси. Може да се твърди, че за моделите от типа (9.12) фактът на съвместимост или несъвместимост на популациите не зависи от първоначалния им брой, а се определя само от естеството на взаимодействието на видовете. Моделът помага да се отговори на въпроса: как трябва да се влияе и управлява биоценозата, за да се унищожат възможно най-бързо вредните видове.
Управлението може да се сведе до краткосрочна, рязка промяна в размера на населението хи вТози метод съответства на методи за контрол като еднократно унищожаване на една или двете популации чрез химически средства. От формулираното по-горе твърдение може да се види, че за съвместими популации този метод на контрол ще бъде неефективен, тъй като с течение на времето системата отново ще влезе в стационарен режим.
Друг начин е да промените вида на функциите на взаимодействие между видовете, например при промяна на стойностите на системните параметри. Именно на този параметричен метод отговарят биологичните методи за контрол. Така с въвеждането на стерилизирани мъжки коефициент на естествения прираст на населението намалява. Ако в същото време получим друг тип фазов портрет, при който има само стабилно стационарно състояние с нулев брой вредители, контролът ще доведе до желания резултат – унищожаването на популацията на вреден вид. Интересно е да се отбележи, че понякога е препоръчително въздействието да се прилага не върху самия вредител, а върху неговия партньор. Като цяло е невъзможно да се каже кой от методите е по-ефективен. Зависи от наличните контроли и от изричната форма на функциите, които описват взаимодействието на популациите.
Моделът на A.D.Bazykin
Теоретичният анализ на моделите на взаимодействия между видовете е най-изчерпателно извършен в книгата на А. Д. Базикин „Биофизика на взаимодействащите популации” (Москва, Наука, 1985).
Помислете за един от моделите хищник-плячка, изследвани в тази книга.
 (9.17)
(9.17)
Системата (9.17) е обобщение на най-простия модел на Волтера хищник-плячка (5.17), като се отчита ефектът от насищането на хищника. В модела (5.17) се приема, че интензивността на изяждане на плячка нараства линейно с увеличаване на плътността на плячката, което не съответства на реалността при висока плътност на плячката. Могат да бъдат избрани различни функции за описване на зависимостта на диетата на хищника от плътността на плячката. Най-важно е избраното да функционира с растеж хасимптотично клони към постоянна стойност. В модела (9.6) е използвана логистичната зависимост. В модела на Базикин като такава функция е избрана хиперболата х/(1+ px). Припомнете си, че това е формата на формулата на Монод, която описва зависимостта на скоростта на растеж на микроорганизмите от концентрацията на субстрата. Тук плячката действа като субстрат, а хищникът действа като микроорганизъм. .
Системата (9.17) зависи от седем параметъра. Броят на параметрите може да бъде намален чрез промяна на променливи:
х® (A/D)х; г ® (A/D)/ y;
т® (1 / А)т; g (9,18)
и зависи от четири параметъра.
За цялостно качествено изследване е необходимо четириизмерното пространство от параметри да се раздели на региони с различни типове динамично поведение, т.е. изградете параметричен или структурен портрет на системата.
След това е необходимо да се построят фазови портрети за всеки от регионите на параметричния портрет и да се опишат бифуркациите, които възникват с фазовите портрети на границите на различни области на параметричния портрет.
Изграждането на пълен параметричен портрет се извършва под формата на набор от „срезове“ (проекции) на параметричен портрет с ниски размери с фиксирани стойности на някои от параметрите.
Параметричен портрет на системата (9.18) с фиксиран жи малки дпоказано на фигура 9.8. Портретът съдържа 10 области с различни типове поведение на фазовата траектория.

Ориз. 9.8.Параметричен портрет на системата (9.18) с фиксиранж
и малки д
Поведението на системата при различни съотношения на параметрите може да бъде значително различно (Фигура 9.9). В системата са възможни следното:
1) едно стабилно равновесие (области 1 и 5);
2) един стабилен пределен цикъл (области 3 и 8);
3) две стабилни равновесия (област 2)
4) стабилен пределен цикъл и нестабилно равновесие вътре в него (области 6, 7, 9, 10)
5) стабилен пределен цикъл и стабилно равновесие извън него (област 4).
В параметрични области 7, 9, 10, областта на привличане на равновесието е ограничена от нестабилен пределен цикъл, лежащ вътре в стабилен. Най-интересен е фазовият портрет, съответстващ на област 6 в параметричния портрет. Той е показан подробно на фиг. 9.10.

Областта на привличане на равновесие В 2 (защрихована) е „охлюв“, усукващ се от нестабилния фокус В 1. Ако е известно, че в началния момент от времето системата е била в близост до B 1, тогава може да се базира само на вероятностни съображения.

Фигура 9.10.Фазов портрет на система 9.18 за параметрична област 6. Областта на привличане В 2 е защрихована
На параметричен портрет(9.7) има 22 различни бифуркационни граници, които се образуват 7 различни видове бифуркации. Тяхното изследване дава възможност да се идентифицират възможни типове поведение на системата при промяна на нейните параметри. Например, когато се движите от района 1 към зона 3 има раждане на малък пределен цикъл или меко раждане на собствени трептения около едно равновесие V.Подобно меко генериране на собствени трептения, но около едно от равновесията, а именно Б 1 , възниква при пресичане на границата на регионите 2 и 4. При излизане от района 4 към зона 5 стабилен пределен цикъл около точкаБ 1 „Избухвания“ в контура на сепаратрисата и равновесието остава единствената привличаща точка Б 2 и т.н.
От особен интерес за практиката, разбира се, е разработването на критерии за близост на системата до границите на бифуркация. Всъщност биолозите са добре запознати със свойството на "буфериране" или "гъвкавост" на естествените екологични системи. Тези термини обикновено означават способността на системата да абсорбира, така да се каже, външни влияния. Докато интензивността на външното влияние не надвишава определена критична стойност, поведението на системата не претърпява качествени промени. Във фазовата равнина това съответства на връщането на системата в стабилно равновесно състояние или към стабилен пределен цикъл, чиито параметри не се различават много от първоначалния. Когато интензивността на въздействието надвиши допустимата стойност, системата се „разпада“, преминава в качествено различен режим на динамично поведение, например просто умира. Това явление съответства на бифуркационен преход.
Всеки тип бифуркационни преходи има свои отличителни черти, които позволяват да се прецени опасността от такъв преход за екосистемата. Ето някои общи критерии, показващи близостта на опасна граница. Както в случая на един вид, ако с намаляване на броя на един от видовете системата „заседне” близо до нестабилна седловина, което се изразява в много бавно възстановяване на броя до първоначалната му стойност, тогава системата е близо до критичната граница. Промяната във формата на колебания в броя на хищниците и плячката също служи като индикатор за опасност. Ако от близки до хармонични трептения се превърнат в релаксация и амплитудата на трептенията се увеличи, това може да доведе до загуба на стабилност на системата и изчезване на един от видовете.
По-нататъшното задълбочаване на математическата теория за взаимодействието на видовете върви по линията на детайлизиране на структурата на самите популации и отчитане на времеви и пространствени фактори.
литература.
Колмогоров A.N. Качествено изследване на математически модели на динамиката на населението. // Проблеми на кибернетиката. М., 1972, бр.5.
Макартър Р. Графичен анализ на екологичните системи // Отдел за доклад по биология Perinceton University. 1971
AD Базикин „Биофизика на взаимодействащите популации“. М., Наука, 1985.
В. Волтера: „Математическата теория на борбата за съществуване“. М.. Наука, 1976
Gause G.F. Борбата за съществуване. Балтимор, 1934 г.
Често представители на един вид (популация) се хранят с представители на друг вид.
Моделът Лотка - Волтера е модел на взаимното съществуване на две популации от типа "хищник - плячка".
Моделът „хищник-плячка” е получен за първи път от А. Лотка през 1925 г., който го използва, за да опише динамиката на взаимодействащите биологични популации. През 1926 г., независимо от Лотка, подобни (при това по-сложни) модели са разработени от италианския математик В. Волтера, чиито задълбочени изследвания в областта на екологичните проблеми поставят основата на математическата теория на биологичните общности, или т.нар. . математическа екология.
В математическа форма предложената система от уравнения има формата:
където x е броят на плячката, y е броят на хищниците, t е времето, α, β, γ, δ са коефициенти, които отразяват взаимодействията между популациите.
Формулиране на проблема
Помислете за затворено пространство, в което има две популации – тревопасни („плячка“) и хищници. Смята се, че животните не се внасят или изнасят и че има достатъчно храна за тревопасните. Тогава уравнението за промяна на броя на жертвите (само жертви) ще приеме формата:
където $ α $ е раждаемостта на жертвите,
$ x $ - размерът на населението на жертвите,
$ \ frac (dx) (dt) $ - темп на нарастване на популацията от жертви.
Когато хищниците не ловуват, те могат да умрат, което означава, че уравнението за броя на хищниците (само хищници) ще приеме формата:
където $ γ $ е степента на загуба на хищници,
$ y $ е размерът на популацията на хищници,
$ \ frac (dy) (dt) $ е темпът на растеж на популацията на хищници.
Когато хищници и плячка се срещнат (честотата на срещите е право пропорционална на продукта), хищниците унищожават плячката с коефициент, добре хранените хищници могат да възпроизвеждат потомство с коефициент. Така системата от уравнения на модела ще има формата:
Решението на проблема
Нека изградим математически модел на съвместното съществуване на две биологични популации от типа "хищник-плячка".
Нека две биологични популации съжителстват в изолирана среда. Средата е неподвижна и осигурява неограничено количество от всичко необходимо за живот на един от видовете – жертвата. Друг вид - хищник - също живее в стационарни условия, но се храни само с плячка. Котки, вълци, щуки, лисици могат да действат като хищници, а пилета, зайци, караси, мишки, съответно, могат да действат като жертви.
За категоричност, нека разгледаме котките в ролята на хищници и пилетата в ролята на плячка.
И така, пилета и котки живеят в някакво изолирано пространство - двор на ферма. Сряда осигурява неограничена храна за пилета, а котките ядат само пилета. Нека означим с
$ x $ - брой пилета,
$ y $ - броят на котките.
С течение на времето броят на пилетата и котките се променя, но ние ще разглеждаме $ x $ и $ y $ като непрекъснати функции на времето t. Нека наречем двойка числа $ x, y) $ състоянието на модела.
Нека открием как се променя състоянието на модела $ (x, y).
Помислете за $ \ frac (dx) (dt) $ - скоростта на промяна в броя на пилетата.
Ако няма котки, тогава броят на пилетата се увеличава и колкото по-бързо, толкова повече пилета. Ще считаме зависимостта за линейна:
$ \ frac (dx) (dt) a_1 x $,
$ a_1 $ е коефициент, който зависи само от условията на живот на пилетата, тяхната естествена смъртност и плодовитост.
$ \ frac (dy) (dt) $ - скоростта на промяна в броя на котките (ако няма пилета), зависи от броя на котките y.
Ако няма пилета, тогава броят на котките намалява (нямат храна) и те умират. Ще считаме зависимостта за линейна:
$ \ frac (dy) (dt) - a_2 y $.
В една екосистема скоростта на промяна в броя на всеки вид също ще се счита за пропорционална на неговия брой, но само с коефициент, който зависи от броя на индивидите от друг вид. Така че за пилетата този коефициент намалява с увеличаване на броя на котките, а за котките се увеличава с увеличаване на броя на пилетата. Също така ще считаме зависимостта за линейна. Тогава получаваме система от диференциални уравнения:

Тази система от уравнения се нарича модел на Волтера-Лотка.
a1, a2, b1, b2 - числови коефициенти, които се наричат параметри на модела.
Както можете да видите, естеството на промяната в състоянието на модела (x, y) се определя от стойностите на параметрите. Чрез промяна на тези параметри и решаване на системата от уравнения на модела е възможно да се изследват закономерностите на промените в състоянието на екологичната система.
Използвайки програмата MATLAB, системата от уравнения на Лотка-Волтера се решава, както следва:
На фиг. 1 е показано решението на системата. В зависимост от началните условия решенията са различни, което отговаря на различни цветове на траекториите.
На фиг. 2 са показани същите решения, но с отчитане на времевата ос t (т.е. наблюдава се зависимост от времето).
Математическото моделиране на биологичните процеси започва със създаването на първите най-прости модели на екологичната система.
Да кажем, че рисовете и зайците живеят в определен затворен район. Рисовете се хранят само със зайци, а зайците - с растителна храна, налична в неограничени количества. Необходимо е да се намерят макроскопските характеристики, които описват популациите. Тези характеристики са броят на индивидите в популациите.
Най-простият модел на връзката между популациите на хищници и плячка, базиран на логистичното уравнение за растеж, е наречен (като модела на междувидовата конкуренция) на своите създатели Лотка и Волтера. Този модел значително опростява изследваната ситуация, но все пак е полезен като отправна точка при анализа на системата хищник-плячка.
Да предположим, че (1) популация на плячка съществува в идеална (независима от плътността) среда, където нейният растеж може да бъде ограничен само от присъствието на хищник, (2) среда, в която съществува хищник, чийто растеж на популацията е ограничен само от изобилието от плячка, е също толкова идеален, (3) и двете популации се възпроизвеждат непрекъснато според уравнението на експоненциалния растеж, (4) скоростта на изяждане на плячка от хищници е пропорционална на честотата на срещите между тях, което от своя страна, е функция от гъстотата на населението. Тези предположения са в основата на модела Лотка-Волтера.
Нека популацията на плячката нараства експоненциално при отсъствие на хищници:
dN / dt = r 1 N 1
където N е броят, а r е специфичният моментен темп на растеж на населението на жертвата. Ако присъстват хищници, тогава те унищожават индивидите на плячката със скорост, която се определя, първо, от честотата на срещите на хищници и плячка, която се увеличава с увеличаване на техния брой и, второ, от ефективността, с която хищникът открива и хваща плячката си при среща. Броят на плячката, срещана и изядена от един хищник N c, е пропорционална на ловната ефективност, която изразяваме чрез коефициента C 1; броя (плътността) на жертвата N и времето, прекарано в търсене Т:
N C = C 1 NT(1)
От този израз е лесно да се определи специфичната скорост на консумация на плячка от хищник (т.е. броят на плячката, изядена от един хищник за единица време), която често се нарича функционална реакция на хищник към плътността на популацията на плячката :
В разглеждания модел C 1е постоянна. Това означава, че броят на плячката, взета от популацията от хищници, нараства линейно с увеличаване на нейната плътност (т.нар. функционален отговор тип 1). Ясно е, че общият процент на изяждане на плячка от всички индивиди на хищника ще бъде:
![]() (3)
(3)
където R -размера на популацията на хищниците. Сега можем да напишем уравнението на растежа за популацията на плячката, както следва:
При липса на плячка индивидите на хищника гладуват и умират. Да предположим също, че в този случай размерът на популацията на хищниците ще намалее експоненциално според уравнението:
![]() (5)
(5)
където r 2- специфична мигновена смъртност в популацията на хищниците.
Ако има жертви, тогава онези индивиди на хищника, които могат да ги намерят и изядат, ще се размножат. Плодовитостта в популацията на хищниците в този модел зависи само от два фактора: скоростта на консумация на плячка от хищника и ефективността, с която консумираната храна се преработва от хищника в неговото потомство. Ако изразим тази ефективност чрез коефициента s, тогава раждаемостта ще бъде:
![]()
Тъй като C 1 и s са константи, тяхното произведение също е константа, която ще означаваме като C 2. Тогава темпът на растеж на популацията на хищниците ще се определи от баланса на плодовитост и смъртност в съответствие с уравнението:
![]() (6)
(6)
Уравнения 4 и 6 заедно образуват модела на Лотка-Волтера.
Можем да изследваме свойствата на този модел по същия начин, както в случая на конкуренция, т.е. чрез конструиране на фазова диаграма, в която броят на плячката е нанесен по ординатата, а този на хищника по абсцисата и начертаване на линии на изоклина, съответстващи на постоянния размер на популацията. С помощта на такива изоклини се определя поведението на взаимодействащите популации от хищник и плячка.
За пострадалото население: откъде
По този начин, тъй като r и С 1 са константи, изоклинът за плячката ще бъде линията, на която се намира номерът на хищника (R)е постоянна, т.е. успоредна на абсцисата и пресичаща ординатата в точката P = r 1 /От 1. Над тази линия броят на жертвите ще намалява, а под тази линия ще се увеличава.
За популацията на хищници:
откъдето
Дотолкова доколкото r 2и С 2 са константи, изоклина за хищника ще бъде линията, на която броят на плячката (N) е постоянен, т.е. перпендикулярна на ординатата и пресичаща абсцисата в точката N = r 2 / C 2. Вляво от него броят на хищника ще намалее, а вдясно ще се увеличи.
Ако разгледаме тези две изоклини заедно, тогава лесно можем да забележим, че взаимодействието на популациите на хищник и плячка е циклично, тъй като техният брой претърпява неограничени конюгирани колебания. Когато броят на плячката е голям, броят на хищниците се увеличава, което води до увеличаване на натиска на хищничеството върху популацията на плячката и по този начин до намаляване на нейния брой. Това намаление от своя страна води до недостиг на храна за хищници и намаляване на техния брой, което води до отслабване на натиска на хищничеството и увеличаване на броя на плячката, което отново води до увеличаване на популацията на плячката, и т.н.
Този модел се характеризира с така наречената "неутрална стабилност", което означава, че популациите извършват един и същ цикъл на колебания за неограничено време, докато някакво външно въздействие промени броя им, след което популациите правят нов цикъл на колебания с различни параметри. ... За да станат циклите стабилни, популациите трябва след външна експозиция стремете се да се върнете към първоначалния цикъл.Такива цикли, за разлика от неутралните стабилни трептения в модела на Лотка-Волтера, обикновено се наричат стабилни гранични цикли.
Моделът на Лотка-Волтера обаче е полезен с това, че позволява да се демонстрира основната тенденция във връзката хищник-плячка, появата на циклични конюгирани флуктуации в размера на техните популации.
Още през 20-те години. А. Лотка и малко по-късно, независимо от него, В. Волтер, предложиха математически модели, описващи спрегнатите флуктуации в броя на хищниците и плячката.
Моделът се състои от два компонента:
С - броят на хищниците; N е броят на жертвите;
Да предположим, че при липса на хищници популацията на плячката ще нараства експоненциално: dN / dt = rN. Но плячката се унищожава от хищници със скорост, която се определя от честотата на срещите между хищник и плячка, а честотата на срещите се увеличава с увеличаване на броя на хищниците (C) и плячката (N). Точният брой на срещната и успешно изядената плячка ще зависи от ефективността, с която хищникът намира и хваща плячка, т.е. от '- "ефективност на търсенето" или "честота на атаките". По този начин честотата на "успешните" срещи между хищник и плячка и следователно скоростта на изяждане на плячка ще бъде равна на a'CN и като цяло dN / dt = rN - a'CN (1 *).
При липса на храна отделните индивиди на хищника губят тегло, гладуват и умират. Да предположим, че в разглеждания модел броят на популацията на хищници при липса на храна ще намалее експоненциално поради гладуване: dC / dt = - qC, където q е смъртността. Смъртта се компенсира от раждането на нови индивиди със скорост, която, както се вярва в този модел, зависи от две обстоятелства:
1) нормата на консумация на храна, a'CN;
2) ефективността (f), с която тази храна преминава в потомството на хищника.
По този начин плодовитостта на хищника е равна на fa'CN и като цяло: dC / dt = fa'CN - qC (2 *). Уравнения 1 * и 2 * съставляват модела на Лотка-Волтер. Могат да се изследват свойствата на този модел, да се конструират линейни изоклини, съответстващи на постоянния размер на популацията, с помощта на такива изоклини може да се определи поведението на взаимодействащите популации хищник-плячка.
В случай на популация жертви: dN / dt = 0, rN = a'CN или C = r / a '. Защото r и a '= const, изоклинът за жертвата ще бъде линията, за която стойността на C е постоянна:
При ниска плътност на хищника (C) броят на плячката (N) се увеличава, а напротив, намалява.
По същия начин за хищници (уравнение 2 *) с dC / dt = 0, fa'CN = qC или N = q / fa ', т.е. Изоклината за хищника ще бъде линията, по която N е постоянна: При висока плътност на плячката популацията на хищника се увеличава, а при ниска плътност намалява.
Техният брой претърпява неограничени спрегнати флуктуации. Когато броят на жертвите е голям, броят на хищниците се увеличава, което води до увеличаване на натиска на хищниците върху популацията на плячката и по този начин до намаляване на нейния брой. Това намаление от своя страна води до ограничаване на хищниците в храната и намаляване на техния брой, което води до отслабване на натиска на хищниците и увеличаване на броя на плячката, което отново води до увеличаване на популацията на хищниците , и т.н.
Популациите извършват един и същ цикъл на колебания за неопределено време, докато някакво външно въздействие промени числеността им, след което популациите извършват нови цикли на неограничени колебания. Всъщност околната среда непрекъснато се променя и броят на населението непрекъснато ще се измества към нови нива. За да са редовни циклите на колебания, които популацията прави, те трябва да са стабилни: ако външно влияние промени нивото на размера на популацията, тогава те трябва да се стремят към първоначалния цикъл. Такива цикли се наричат стабилни, гранични цикли.
Моделът на Лотка-Волтер ни позволява да покажем основната тенденция във връзката хищник-плячка, която се изразява в появата на колебания в изобилието в популацията на плячката, придружени от колебания в изобилието в популацията на хищници. Основният механизъм на такива флуктуации е забавянето във времето, присъщо на последователността на състоянието от голям брой плячка до голям брой хищници, след това до малък брой плячка и нисък брой хищници, до голям брой плячка , и т.н.
5) ПОПУЛАЦИОННИ СТРАТЕГИИ НА ХИЩНИК И ЖЕРТВА
Връзката хищник-плячка представлява връзките в процеса на пренос на материя и енергия от фитофагите към зоофагите или от хищници от по-нисък ред към хищници от по-висок ред. от естеството на тези взаимоотношения разграничава три варианта на хищници:
а) колекционери... Хищникът събира достатъчно малки мобилни жертви. Този вид хищничество е характерно за много видове птици (зубици, чинки, кънки и др.), които изразходват енергия само за търсене на плячка;
б) истински хищници... Хищникът преследва и убива жертвата;
v) пашари... Тези хищници използват плячката си много пъти, например слепи или конски мухи.
Стратегията за получаване на храна от хищници е насочена към осигуряване на енергийна ефективност на храненето: консумацията на енергия за получаване на храна трябва да бъде по-малка от енергията, получена по време на нейното усвояване.
Истински хищницисе разделят на
„Жътвари“, които се хранят с изобилие от ресурси (n, планктонна риба и дори мустакат кит), и „ловци“, които получават по-малко изобилна храна. На свой ред
„Ловците“ са разделени на „засади“, улавящи плячка (например щука, ястреб, котка, бръмбар богомол), „търсачи“ (насекомоядни птици) и „преследвачи“. За последната група търсенето на храна не изисква големи разходи на енергия, но е необходимо много, за да завладее жертвата (лъвове в саваните). Въпреки това, някои хищници могат да комбинират стратегически елементи от различни опции за лов.
Както в случая на връзката фитофаг-растение, в природата не се наблюдава ситуация, при която цялата плячка ще бъде изядена от хищници, което в крайна сметка ще доведе до тяхната смърт. Екологичен баланс между хищници и плячка се поддържа от специални механизминамаляване на риска от пълно унищожаване на жертвите. Така че жертвите могат:
Бягайте от хищника. В този случай в резултат на адаптациите се увеличава мобилността както на плячката, така и на хищниците, което е особено характерно за степните животни, които няма къде да се скрият от преследвачите си;
Придобийте защитен цвят („преструвайте се“ на листа или клонки) или, напротив, ярък цвят, N: червено, предупреждавайки хищника за горчив вкус. Добре известно е, че цветът на заека се променя през различни периоди на годината, което му позволява да се маскира в тревата през лятото и на фона на бял сняг през зимата. Адаптивната промяна на цвета може да настъпи на различни етапи от онтогенезата: малките на тюлените са бели (цветът на снега), а възрастните са черни (цветът на скалистия бряг);
Разпространение на групи, което прави търсенето и риболова на хищник по-енергийно интензивни;
Скрийте се в прикритие;
Да се премине към мерки за активна защита (тревопасни животни, с рога, бодливи риби), понякога ставни (мускусните волове могат да поемат „защита на периметъра“ от вълци и др.).
От своя страна хищниците развиват не само способността бързо да преследват плячката, но и обонянието, което позволява да се определи местоположението на плячката по миризма. Много видове хищници разбиват дупките на плячката си (лисици, вълци).
В същото време самите те правят всичко възможно, за да не открият присъствието им. Това обяснява чистотата на малките котки, които прекарват много време в тоалетната и заравят екскрементите, за да премахнат миризмата. Хищниците носят "камуфлажни одежди" (райета щука и костур, което ги прави по-малко забележими в гъсталаците на макрофити, раирани тигри и др.).
Пълна защита от хищници на всички индивиди в популациите на плячката също не се осъществява, тъй като това би довело не само до смъртта на гладуващите хищници, но в крайна сметка до катастрофа на популациите плячка. В същото време, при липса или намаляване на гъстотата на популацията на хищници, генофондът на популацията на плячката се влошава (остават болни и стари животни) и поради рязкото увеличаване на техния брой хранителните доставки се подкопана.
Поради тази причина рядко се наблюдава ефектът от зависимостта на броя на плячката и популациите на хищници - пулсирането на популацията на плячката, последвано от пулсиране на популацията на хищници с известно закъснение („ефект на Лотка - Волтера“).
Установява се доста стабилно съотношение между биомасите на хищници и плячка. Така Р. Рикълфс цитира данни, че съотношението на биомасите на хищник и плячка варира от 1:150 - 1:300. В различни екосистеми на умерения пояс на САЩ има 300 малки белоопашати елени (тегло 60 кг), 100 големи елена уапити (тегло 300 кг) или 30 лоса (тегло 350) на вълк. Същият модел е открит и в саваните.
При интензивна експлоатация на популации от фитофаги човек често изключва хищници от екосистемите (в Обединеното кралство например има сърни и елени, но няма вълци; в изкуствени водоеми, където се отглеждат шарани и други езерни риби, няма щуки ). В този случай ролята на хищник се изпълнява от самия човек, отнемайки част от индивидите от популацията на фитофаги.
Специален вариант на хищничество се наблюдава при растенията и гъбите. В растителното царство има около 500 вида, които са в състояние да улавят насекоми и частично да ги усвояват с помощта на протеолитични ензими. Хищните гъби образуват улавящи устройства под формата на малки овални или сферични глави, разположени върху къси клони на мицела. Въпреки това, най-често срещаният тип капан е лепкава триизмерна мрежа, състояща се от голям брой пръстени, образувани в резултат на разклоняването на хифите. Хищните гъби могат да уловят доста големи животни, като кръгли червеи. След като червеят се оплете в хифите, те растат в тялото на животното и бързо го запълват.
1.Постоянно и благоприятно ниво на температура и влажност.
2. Изобилие от храна.
3. Защита от неблагоприятни фактори.
4. Агресивен химичен състав на местообитанието (храносмилателни сокове).
1. Наличието на две местообитания: среда от първи ред - организмът на гостоприемника, среда от втори ред - външната среда.
